A distributor receives a large shipment of components. The distributor would like to accept the shipment if 10% or fewer of the components are defective and to return it if more than 10% of the components are defective. She decides to sample 10 components, and to return the shipment if more than 1 of the 10 is defective.
a. If the proportion of defectives in the batch is in fact 10%, what is the probability that she will return the shipment?
b. If the proportion of defectives in the batch is 20%, what is the probability that she will return the shipment?
c. If the proportion of defectives in the batch is 2%, what is the probability that she will return the shipment?
d. The distributor decides that she will accept the shipment only if none of the sampled items are defective. What is the minimum number of items she should sample if she wants to have a probability no greater than 0.01 of accepting the shipment if 20% of the components in the shipment are defective?
(a) Let X be the number of components out of 10 that are defective. Then X~ Bin(10,0.1).
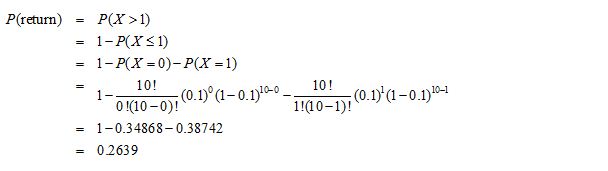
(b) Let X be the number of components out of 10 that are defective. Then X ~ Bin(10,0.2).
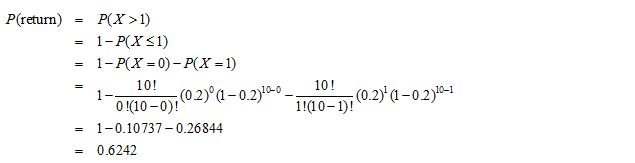
(c) Let X be the number of components out of 10 that are defective. Then X ~ Bin(10,0.02).
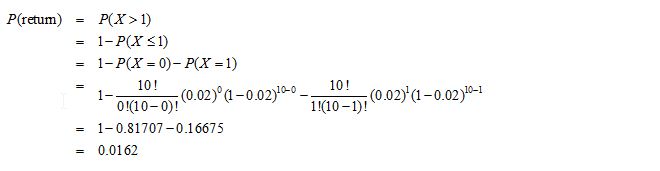
(d) Let n be the required sample size. Let X be the number of sampled components that are defective. Then X ~ Bin(n, 0.2).
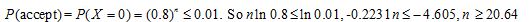
The minimum sample size is 21.
You might also like to view...
What are the two factors responsible for genetic variation in animals?
What will be an ideal response?
In the accompanying figure, R=90? and L=0.319H. Calculate the total impedance.
What will be an ideal response?
To avoid electrical shock, what class fire extinguisher should be used on electrical equipment?
A) Class A B) Class B C) Class C D) Class D
If a machine has an equalizer bar it will:
a. ensure both tracks turn at the same speed during straight travel b. make removing the track frame easier c. allow the track frames to pivot slightly d. keep the track frames rigid at all times