Simplify.-14 - 0 - 5 - (-2) + 17
A. -4
B. 6
C. -28
D. 0
Answer: D
You might also like to view...
Find the linear approximation of the function at the given point.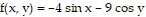
at 
A. 
B.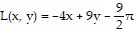 
C. 
D.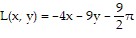 
The given situation involves a rate of change that you may assume to be constant. Write a statement that describes how one variable varies with respect to another, give the rate of change numerically (with units), and use the rate of change rule to answer the questions.A gas station owner finds that for every penny increase in the price of gasoline, she sells 1657 fewer gallons of gas per week. How much more or less gas will she sell if she raises the price by 6 cents per gallon? If she decreases the price by 2 cents per gallon?
A. At a particular gas station, sales decrease with respect to price by 1657 gallons per cent. The rate of change is -1657 gallons per cent. If the price is increased by 6 cents per gallon, the change in gas sales is -9942 gallons. If the price is decreased by 2 cents, gas sales increase by 3314 gallons. B. At a particular gas station, sales decrease with respect to price by 1657 gallons per cent. The rate of change is 1657 gallons per cent. If the price is increased by 6 cents per gallon, the change in gas sales is 7456.5 gallons. If the price is decreased by 2 cents, gas sales increase by 2485.5 gallons. C. At a particular gas station, sales decrease with respect to price by 1657 gallons per cent. The rate of change is -1657 gallons per cent. If the price is increased by 6 cents per gallon, the change in gas sales is -12,427.5 gallons. If the price is decreased by 2 cents, gas sales increase by -4142.5 gallons. D. At a particular gas station, sales decrease with respect to price by 1657 gallons per cent. The rate of change is 1657 gallons per cent. If the price is increased by 6 cents per gallon, the change in gas sales is 4971 gallons. If the price is decreased by 2 cents, gas sales increase by -1657 gallons.
Provide an appropriate response.Urban encroachment is causing the area of a forest to decline at a rate of 3% per year. Use the approximate half-life formula to determine the fraction that remains in 63 years.
A. 0.535887 B. 0.970731 C. 1.350000 D. 0.153893
Solve the problem. Round your answer to 5 decimal places when necessary.The table shows the leading causes of death for one country in a single recent year. 
Assume a population of 75.5 million.In a typical city of 500,000 , how many people would you expect to die by accident in a year?
A. Approximately 225 people B. Approximately 2250 people C. Approximately 16,987.5 people D. Approximately 1699 people