Solve the problem.Assume that the seed square of the Sierpinski carpet has area A = 1. Find the area of the "carpet" obtained in step 5 of the construction.
A. 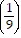 5
5
B. 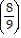 5
5
C. 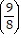 5
5
D. 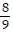
E. 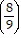 4
4
Answer: B
You might also like to view...
Find the absolute maxima and minima of the function on the given domain.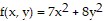 on the disk bounded by the circle
on the disk bounded by the circle 
A. Absolute maximum: 72 at 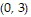 and
and 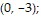 absolute minimum: 63 at
absolute minimum: 63 at  and
and 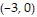
B. Absolute maximum: 72 at  and
and 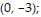 absolute minimum: 0 at
absolute minimum: 0 at 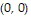
C. Absolute maximum: 135 at  absolute minimum: 0 at
absolute minimum: 0 at 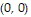
D. Absolute maximum: 63 at 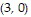 and
and 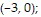 absolute minimum: 0 at
absolute minimum: 0 at 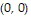
Simplify using order of operations.(-12)2 ? (4 - 7)2 ÷ 33
A. 48 B. -64 C. 64 D. -48
Identify a method whereby a random sample can be selected from the population.The organizer of a contest would like to select a random sample of 20 prizewinners from the 627 contestants who correctly answered all questions.
A. Select the first 20 contestants whose names begin with the letter C. B. Choose the 20 responses which have the earliest postmark. C. Construct a spinner with ten 36° sectors numbered 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Assign each contestant a number from 001 to 627. Generate a random sequence of three-digit numbers by repeatedly spinning the spinner 3 times. Ignore any number greater than 627, any number already obtained, or 000. When 20 appropriate numbers have been generated, they can be used to identify the contestants to be included in the sample.
Find the Taylor series for the given function.f(x) = x8 ex
A. 
B. 
C. 
D. 