Suppose that the rate at which a nuclear power plant produces radioactive waste is proportional to the number of years it has been operating, according to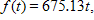 
in pounds per year. Suppose also that the waste decays exponentially at a rate of 6% per year. Then the amount of radioactive waste that will accumulate in b years is given by
src="https://sciemce.com/media/3/ppg__cognero__Chapter_13_Definite_Integrals_Techniques_of_Integration__media__9bbc2c46-63ba-45c9-af0e-3f5a3a45568b.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_9982ce11186045cf8903fa89b" /> and this integral evaluates to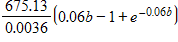 
. How much waste will accumulate in the long run? Take the limit as 
in the integral evaluated. Round your answer to the nearest pound, if it exists.
?
A. Approximately 187,536 pounds of waste will accumulate in the long run.
B. Approximately 11,252 pounds of waste will accumulate in the long run.
C. Approximately 176,284 pounds of waste will accumulate in the long run.
D. 0 (No waste will accumulate in the long run.)
E.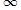 
(Waste is produced more rapidly than existing waste decays.)
Answer: E
Mathematics
src="https://sciemce.com/media/3/ppg__cognero__Chapter_13_Definite_Integrals_Techniques_of_Integration__media__9bbc2c46-63ba-45c9-af0e-3f5a3a45568b.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_9982ce11186045cf8903fa89b" /> and this integral evaluates to 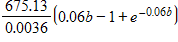. How much waste will accumulate in the long run? Take the limit as in the integral evaluated. Round your answer to the nearest pound, if it exists.
?
A. Approximately 187,536 pounds of waste will accumulate in the long run.
B. Approximately 11,252 pounds of waste will accumulate in the long run.
C. Approximately 176,284 pounds of waste will accumulate in the long run.
D. 0 (No waste will accumulate in the long run.)
E. 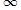(Waste is produced more rapidly than existing waste decays.)
Answer: E
You might also like to view...
Evaluate the indicated double integral over R.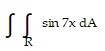
; R = {(x, y): 0 ? x ? 
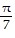, 0 ? y ? ?}
A.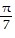 
B. ?
C.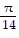 
D.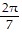 
Evaluate the definite integral.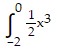
dx
A. - 2 B. 2 C. 8 D. - 8
Simplify. Assume that all variables represent positive numbers.
A. 8k7q8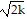 
B. 8k3q4 
C. 8q4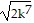 
D. 8k3q4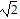 
Find the net cost equivalent and the percent form of the single discount equivalent for the following series discount.10/5/20
A. 0.316; 68.4% B. 0.7; 35% C. 0.35; 70% D. 0.684; 31.6%