Integrate the function.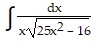
A.  sec-1
sec-1  x + C
x + C
B.  sec-1
sec-1 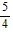 x + C
x + C
C. 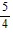 sin-1
sin-1 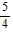 x + C
x + C
D. 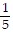 sin-1
sin-1 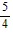 x + C
x + C
Answer: A
You might also like to view...
Find the absolute maxima and minima of the function on the given domain. on the diamond-shaped region
on the diamond-shaped region 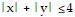
A. Absolute maximum:  at
at 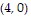 and
and 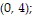 absolute minimum: 0 at
absolute minimum: 0 at  and
and 
B. Absolute maximum:  at
at 

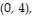 and
and  absolute minimum: 8 at
absolute minimum: 8 at 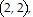

 and
and 
C. Absolute maximum: 8 at 

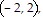 and
and  absolute minimum: 0 at
absolute minimum: 0 at 
D. Absolute maximum:  at
at 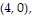

 and
and  absolute minimum: 0 at
absolute minimum: 0 at 
Solve the problem.The volume V of a 10-gram object varies inversely with the density d in grams per milliliters, 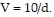 Find
Find 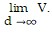 Interpret your answer.
Interpret your answer.
A. ?, As the density of the object becomes infinitely large, the volume of the object becomes infinitely large. The more compact the object is, the more space it takes up. B. 10, As the density of the object becomes infinitely large, the volume of the object approaches a limit of 10 milliliters. As the object gets more and more compact, its volume becomes 10 milliliters. C. 1, As the density of the object becomes infinitely large, the volume of the object approaches a limit of 1 milliliter. As the object gets more and more compact, its volume diminishes to 1 milliliter. D. 0, As the density of the object becomes infinitely large, the volume of the object approaches a limit of 0 milliliters. The more compact the object is, the less space it takes up.
Solve the inequality.(a + 4)(a - 4)(a - 5) > 0
A. (-4, 4) or (5, ?) B. (5, ?) C. (-?, -4) or (4, 5) D. (-?, 4)
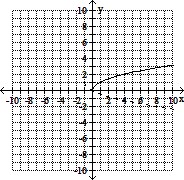
Sketch the requested graphs.Begin by graphing the standard square root function f(x) = 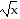 as a solid curve. Then use transformations of this graph to graph the function g(x) =
as a solid curve. Then use transformations of this graph to graph the function g(x) = 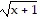 + 1 as a dashed curve.
+ 1 as a dashed curve.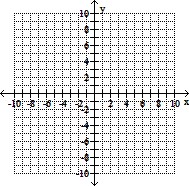
A. 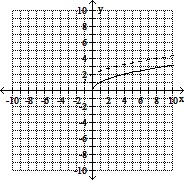
B. 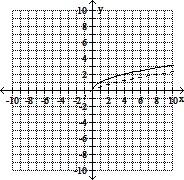
C. 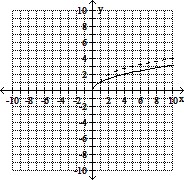
D.