Use mathematical induction to prove that the statement is true for every positive integer n.3 + 3 ? 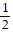 + 3 ?
+ 3 ? 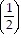 2 + ... + 3 ?
2 + ... + 3 ? 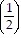 n - 1 =
n - 1 = 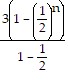
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 3 = 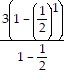 =
= 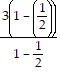 = 3. Thus, the statement is true for n = 1.
= 3. Thus, the statement is true for n = 1.
b). Assume that the statement is true for n = k:
Sk = 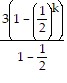
Also, if the statement is true for n = k + 1, then
Sk+1 = Sk + 3 ? 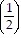 (k+1) - 1=
(k+1) - 1= 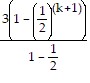
Substitute the expression for Sk into the one for Sk+1:
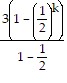 + 3 ?
+ 3 ? 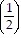 (k+1) - 1=
(k+1) - 1= 
Collect the terms on the left-hand side over a common denominator:
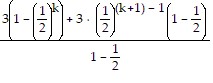 =
= 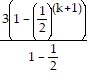
Expand the numerator of the left-hand side and simplify to get:
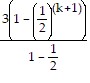 =
= 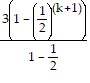
Since the equality holds, the statement is true for n = k + 1 as long as it is true for n = k. Furthermore, the statement is true for n = 1. Thus, the statement is true for all natural numbers n.
You might also like to view...
What is the difference between a rotation and a translation? ?
A. ?A rotation "revolves" a certain number of degrees while a translation shifts horizontally or vertically. B. ?A rotation shifts horizontally while a translation "revolves" a certain number of degrees. C. ?A rotation shifts vertically while a translation "revolves" a certain number of degrees. D. ?A rotation "revolves" a certain number of degrees while a translation "reflects" across a line. E. ?A rotation "revolves" and "reflects" while a translation only "reflects".
Provide an appropriate response.When using the substitution or elimination method to solve a system of two equations, you end up with an equation stating 0 = 7. What does this indicate to you about the system of equations?
What will be an ideal response?
Decide whether the ordered pair is a solution of the given system.(4, -2)x + y = -6x - y = -2
A. Yes B. No
Write in radical form. Assume all variables represent positive real numbers.x1/7
A. 
B. 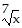
C. 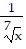
D. x-7