Use the boundedness theorem to determine whether the polynomial function satisfies the given condition.The polynomial f(x) = x5 - 5x3 + 4x has no real zero greater than 2.
A. Yes, the boundedness theorem shows that the polynomial has no real zero greater than 2.
B. No, the boundedness theorem does not show that the polynomial has no real zero greater than 2.
Answer: B
You might also like to view...
Simplify.(60 - 18) ? [(80 + 20 ÷ 5) - (8 ? 8 - 5 ? 5)]
A. 1,990 B. 1,854 C. 1,947 D. 1,890
Simplify.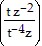
-2
A.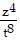 
B.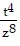 
C.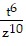 
D. 
A local newspaper charges $18 for the first 3 lines of a want ad, and then $6.50 for each additional line. Express the cost of an x-line ad, c(x), as a piecewise function.
What will be an ideal response?
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.(x - 3)2 - 25(y + 2)2 = 25
A. center at (3, -2)
transverse axis is parallel to x-axis
vertices at (2, -2) and (4, -2)
foci at (3 -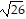 
, -2) and (3 + 
, -2)
asymptotes of y + 2 = - 5(x - 3) and y + 2 = 5(x - 3)
B. center at (3, -2)
transverse axis is parallel to y-axis
vertices at (3, -7) and (3, 3),
foci at (3, -2 -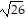 
) and (3, -2 + 
),
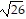asymptotes of y - 2 = - 5(x + 3) and y - 2 = 5(x + 3)
C. center at (-2, 3)
transverse axis is parallel to x-axis
vertices at (-7, 3) and (3, 3)
foci at (-2 -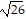 
, 3) and (-2 + 
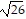, 3)
asymptotes of y - 3 = -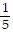 
(x + 2) and y - 3 = 
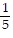(x + 2)
D. center at (3, -2)
transverse axis is parallel to x-axis
vertices at (-2, -2) and (8, -2)
foci at (3 -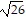 
, -2) and (3 + 
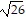, -2)
asymptotes of y + 2 = -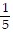 
(x - 3) and y + 2 = 
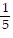(x - 3)