A random sample of adult female reaction times has a sample mean of x¯=394.3 milliseconds and sample standard deviation of s=84.6 milliseconds. Use the Empirical Rule to determine the approximate percentage of adult female reaction times that lie between 140.5 and 648.1 milliseconds.
Answer:
Given that ,
mean = \mu = 394.3
standard deviation = \sigma = 84.6
Using z table,
P(140.5< x <648.1 ) = P[(140.5 - 394.3) / 84.6< (x -\mu) / \sigma < (648.1 - 394.3) /84.6 )]
= P( -3< Z < 3)
= P(Z <3 ) - P(Z < -3)
using empirical rule
99.7%=\mu + / - 2 =99.7 / 2=49.85%
99.7%=\mu + / - 2 =99.7 / 2=49.85%
P(Z <3 ) + P(Z < -3)
=49.85% +49.85%
=99.7%
You might also like to view...
Add or subtract as indicated. Write the answer in lowest terms.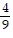 +
+ 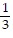 -
- 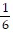
A. 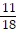
B. 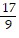
C. 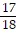
D. 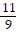
The following chart shows some figures from an income statement. Prepare a vertical analysis by expressing each item as a percent of net sales. Round percents to the nearest tenth of a percent.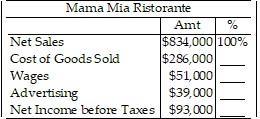
A. 34.3%, 17.8%, 13.6%, 32.5% B. 34.3%, 6.1%, 76.5%, 11.2% C. 34.3%, 6.1%, 4.7%, 11.2% D. 34.3%, 6.2%, 13.6%, 32.5%
Find the probability of the compound event.Two 6-sided dice are rolled. What is the probability that the sum is odd and the number on one of the dice is a 1?
A. 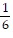
B. 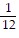
C. 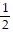
D. 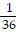
Solve the problem.An 8-cylinder Crown Victoria gives 18 miles per gallon in city driving and 21 miles per gallon in highway driving. A 300-mile trip required 15.5 gallons of gasoline. How many whole miles were driven in the city?
A. 153 miles B. 132 miles C. 147 miles D. 168 miles