The graphs show the position s, velocity v = ds/dt, and acceleration a = d2s/dt2 of a body moving along a coordinate line as functions of time t. Which graph is which?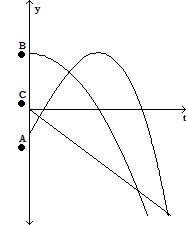
A. A = position, C = velocity, B = acceleration
B. A = position, B = velocity, C = acceleration
C. B = position, A = velocity, C = acceleration
D. C = position, A = velocity, B = acceleration
Answer: B
You might also like to view...
Find a Cartesian equation for the line whose polar equation is given.r cos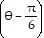 = 4
= 4
A. y = 8 -  x
x
B. y = 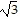 x + 4
x + 4
C. y = 8 -  x
x
D. y = 4 -  x
x
Express the number in standard notation.1.11 × 10-4
A. -111,000 B. 0.00111 C. 0.000111 D. 0.0000111
Find the requested angle.Supplement of 166°
A. 76° B. 14° C. 194° D. 332°
Solve the following quadratic application using the given graph. The profit that the vendor makes per day by selling x pretzels is given by the function  (i) Find the number of pretzels that must be sold to maximize profit. (ii) What is the maximum profit? (iii) Write the vertex as an ordered pair. (iv) Write the x-intercepts as ordered pairs. What are the real-world meanings of the intercepts?
(i) Find the number of pretzels that must be sold to maximize profit. (ii) What is the maximum profit? (iii) Write the vertex as an ordered pair. (iv) Write the x-intercepts as ordered pairs. What are the real-world meanings of the intercepts?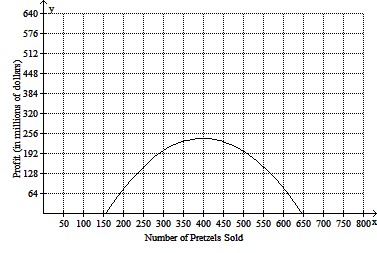
A. (i) 800 pretzels must be sold to maximize profit. (ii) The maximum profit is $80 million. (iii) Vertex: (800, 80) (iv) x-intercepts: (0, 155.05) and (0, 644.95). There is no profit when 155.05 and 644.95 pretzels are sold. B. (i) 80 pretzels must be sold to maximize profit. (ii) The maximum profit is $800 million. (iii) Vertex: (80, 800) (iv) x-intercepts: (0, 310.1) and (0, -644.95). There is no profit when 310.1 and -644.95 pretzels are sold. C. (i) 240 pretzels must be sold to maximize profit. (ii) The maximum profit is $400 million. (iii) Vertex: (240, 400) (iv) x-intercepts: (0, 310.1) and (0, -644.95). There is no profit when 310.1 and -644.95 pretzels are sold. D. (i) 400 pretzels must be sold to maximize profit. (ii) The maximum profit is $240 million. (iii) Vertex: (400, 240) (iv) x-intercepts: (0, 155.05) and (0, 644.95). There is no profit when 155.05 and 644.95 pretzels are sold.