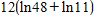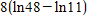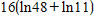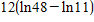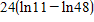Solve the problem.A team of engineers is testing an experimental high-voltage fuel cell with a potential application as an emergency back-up power supply in cell phone transmission towers. Unfortunately, the voltage of the prototype cell drops with time according to the equation 
where V is in volts and t is the time of operation in hours. The cell provides useful power as long as the voltage remains above volts. Use Newton's method to find the useful working time of the cell to the nearest tenth of an hour (that is, solve V(t) = 1.5 volts). Use t = 7 hours as your initial guess and show all your work.
What will be an ideal response?
Find the root of f(x) = -0.0306t3 + 0.373t2 - 2.16t + 15.1 - 1.5.
f'(x) = -0.0918t2 + 0.746t - 2.16
x1 = 7
x2 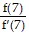= 7 - 
= 7 -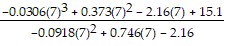 
= 12.40
x3 = 12.40 -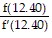 
= 12.40 - 
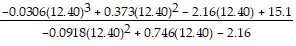= 10.60
The useful working time is t = 10.60 hours.
You might also like to view...
Solve the problem.How many 5-card poker hands consisting of three 4's and two cards that are not 4's are possible in a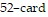 
deck?
A. 2256 B. 2652 C. 5304 D. 4512
Simplify the expression by combining like terms if possible.7x2 - 5 + 5x2 + 4
A. 11 B. 11x2 C. 12x2 - 1 D. 2x2 - 1
Evaluate the integral.
?
?
A. 
B. 
C. 
D. 
E. 
Solve the problem.The revenue received from the sale of electric heaters is seasonal, with maximum revenue in the winter. Let the revenue received from the sale of heaters be approximated by R(x) = 90 cos 2?x + 600, where x is time in years, measured from January 1. Find R'(x) for March 1st.
A. -90?
B. -90?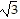
C. -90?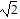
D. 0