Solve the problem.A small manufacturing plant produces two kinds of bicycles, three-speed and ten-speed, in two factories. Factory A produces 16 three-speeds and 20 ten-speeds in one day, whereas factory B produces 12 three-speeds and 20 ten-speeds in one day. An order is received for 96 three-speeds and 140 ten-speeds. It costs $1000 a day to operate factory A and $800 a day to operate factory B. How many days should the manufacturer operate each factory in order to fill the order at minimum cost?For the linear programming problem above:(a) Define the variables.(b) Write the system of linear inequalities that must be satisfied.(c) Write the cost function. (d) Determine the feasible set. Label each boundary with its equation.(e) Solve the problem.
src="https://sciemce.com/media/4/ppg__rrr0625191404__f1q47g1.jpg" alt="" style="vertical-align: 0.0px;" height="200" width="200" />
What will be an ideal response?
(a) x = number of days the manufacturer operates factory A
y = number of days the manufacturer operates factory B
(b)
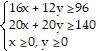
(c) 1000x + 800y
(d)
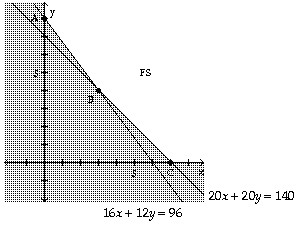
(e) The manufacturer should operate factory A for 3 days and factory B for 4 days in order to fill the order at a minimum cost of $6200.
Mathematics
src="https://sciemce.com/media/4/ppg__rrr0625191404__f1q47g1.jpg" alt="" style="vertical-align: 0.0px;" height="200" width="200" />
What will be an ideal response?
| (a) | x = number of days the manufacturer operates factory A |
(b)
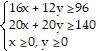
| (c) | 1000x + 800y |

(e) The manufacturer should operate factory A for 3 days and factory B for 4 days in order to fill the order at a minimum cost of $6200.
You might also like to view...
Use a finite approximation to estimate the area under the graph of the given function on the stated interval as instructed.f(x) = x2 between x = 3 and x = 7 using an upper sum with four rectangles of equal width.
A. 86 B. 117 C. 126 D. 105
Solve the equation.
?

A. 2, 7 B. 4, 5 C. ?1, 8 D. no solution E. -7, 2
Many states conduct lotteries; a typical lottery payoff ticket is shown here. Assume there are 20 numbers chosen from a set of 80 possible numbers. What is the expectation for a five-spot game? Assume that the ticket cost $1. 5 SPOT GAMEMATCHPRIZE543$270$30$4?
A. $0.13 B. $0.26 C. - $0.13 D. $0.25 E. - $0.26
Solve the system of equations using the inverse of the coefficient matrix.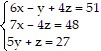
A. x = 8, y = 2, z =5 B. x = 8, y = 5, z = 2 C. x = -8, y = 5, z = 16 D. The system is inconsistent.