Solve the problem using your calculator.Ten students in a graduate program were randomly selected. Their grade point averages (GPAs) when they entered the program were between 3.5 and 4.0. The following data were obtained regarding their GPAs on entering the program versus their current GPAs. Use linear regression to find a linear function that predicts a student's current GPA as a function of his or her entering GPA. Entering GPA Current GPA 3.5 3.6 3.8 3.7 3.6 3.9 3.6 3.6 3.5 3.9 3.9 3.8 4.0 3.7 3.9 3.9 3.5 3.8 3.7 4.0
A. y = 2.51 + 0.329x
B. y = 5.81 + 0.497x
C. y = 3.67 + 0.0313x
D. y = 4.91 + 0.0212x
Answer: C
You might also like to view...
Provide an appropriate response.Evaluate: 20 - 10 ÷ 5 + 23
Fill in the blank(s) with the appropriate word(s).
Solve the inequality and graph the solution.12 + 12t + 11 ? 11t + 22![]()
A. (12, ?)![]()
B. [ -1, ?)![]()
C. (-?, 12)![]()
D. (-?, -1]![]()
Solve the equation. x =
x = 
A. 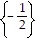
B. {2}
C. 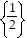
D. {-2}
Provide an appropriate response.A second derivative will not exist for a function at a point if  .
.
A. The function is not defined at the point, the first derivative is discontinuous at the point; the first derivative has a corner or similar sharp change in direction at the point; the first derivative has a vertical tangent at the point. B. The first derivative is not defined at the point; the first derivative is discontinuous at the point; the first derivative has a corner or similar sharp change in direction at the point; or the first derivative has a horizontal tangent at the point. C. The first derivative is not defined at the point, the first derivative is discontinuous at the point, the first derivative has a limit at the point; or the function has a vertical tangent at the point. D. The function is not defined at the point, the function is discontinuous at the point; the first derivative has a peak or a valley at the point, or the function has a vertical tangent at the point.