Provide an appropriate response.Plot the functions u(x) = 9, l(x) = 9 - x2, and f(x) = 8 + cos2x. Then use these graphs along with the Squeeze Theorem to prove that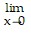 
f(x) = 9 .
What will be an ideal response?
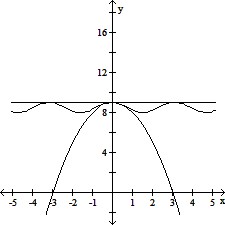
From the graph, it can be seen that the graph of f(x) = 8 + cos2 x is between the graphs of l(x) = 9 - x2 and u(x) = 9. Also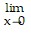 
l(x) = 9 and 
u(x) = 9. Since the graph of f(x) = 8 + cos2x is squeezed between the graphs of 
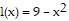and u(x) = 9, both of which go to 9 as x?0, by the Squeeze Theorem we can conclude that 
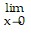f(x) = 9.
You might also like to view...
Find the extreme values of the function subject to the given constraint.
A. Maximum: 81 at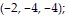 
minimum: 9 at 
B. Maximum: 77 at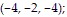 
minimum: 13 at 
C. Maximum: 49 at 
minimum: 41 at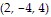 
D. Maximum: 77 at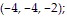 
minimum: 13 at 
Provide an appropriate response.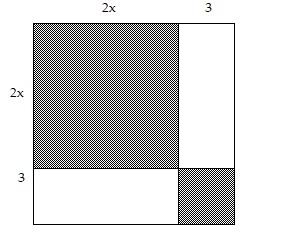
Find the total area.
A. 4x2 + 6x + 9 B. 4x2 + 12x + 9 C. 2x2 + 12x + 9 D. 2x2 + 6x + 9
Tell whether the pair of ratios forms a proportion. Answer yes or no.
?
,
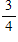
What will be an ideal response?
Solve the compound inequality. Express the solution using interval notation. Graph the solution set.x ? 5 and x ? 4
A. [4, ?)
B. [4, 5]
C. (-?, 4]
D. (-?, 4] ? [5, ?)