Solve the given differential equation (where the function is subject to the given conditions) by using Laplace transforms.y" + 4y' + 4y = e-2t, y = 1, y'
= 1, y'  = 4
= 4
A. y = e2t
B. y = e-2t
C. y = e-2t
D. y = e-2t
Answer: C
You might also like to view...
Solve.The sum of the squares of the digits of a positive two-digit number is 61, and the tens digit is 1 more than the units digit. Find the number.
A. 54 B. 65 C. 45 D. 56
Find a power function that models the data in the table. Round to three decimal places if necessary.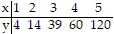
A. y = 27.8x - 36 B. y =2.085x3.734 C. y = 3.734x2.085 D. y = 2.309x2.284
Solve the problem.Find the standard form of the equation of the circle. Assume that the center has integer coordinates and the radius is an integer. 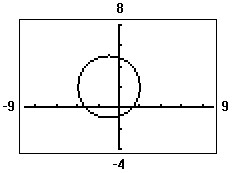
A. (x + 1)2 + (y - 2)2 = 9 B. x2 + y2 + 2x - 4y - 4 = 0 C. (x - 1)2 + (y + 2)2 = 9 D. x2 + y2 - 2x + 4y - 4 = 0
Use the tables to evaluate the expression if possible.Find (f ? g)(7). 

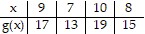
A. 7 B. 13 C. 30 D. 26