Answer the question.You are hiking on a mountainside, following a trail that slopes downward for a short distance and then begins to climb again. At the bottom of this local "dip", what can be said about the relationship between the trail's direction and the contour of the mountainside? [Hint - Think of the trail as a constrained path, g(x, y) = c, on the mountainside's surface, altitude = f(x, y). Consider only infinitesimal displacements.]
A. At the bottom of the dip, the trail is headed along the mountain's contour line which passes through that point.
B. At the bottom of the dip, the trail is headed perpendicular to the mountain's contour line which passes through that point.
C. At the bottom of the dip, the trail is headed in the direction of the mountain's steepest ascent.
D. The mountainside rises in all directions relative to the dip.
Answer: A
You might also like to view...
Solve the problem.Suppose that the parametrized plane curve C: (f(u), g(u)) is revolved about the x-axis, where g(u) > 0 and a ? u ? b. Show that the surface area of the surface of revolution is 2?
du
What will be an ideal response?
Find the exact value under the given conditions.sin ? =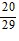 
, 0 < ? < 
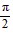; cos ? = 
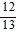, 0 < ? < 
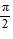Find cos (? + ?).
A.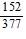 
B.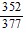 
C.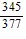 
D.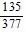 
Use the graph to identify domain and range.
A. domain: (-?, ?) range: (-4, ?) B. domain: [-4, ?) range: (-?, ?) C. domain: (-4, ?) range: (-?, ?) D. domain: (-?, ?) range: [-4, ?)
Factor completely. If the polynomial cannot be factored, say it is prime.18x2 - 78x - 60
A. (18x + 12)(x - 5) B. 6(3x - 2)(x + 5) C. 6(3x + 2)(x - 5) D. prime