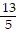Solve the problem.North American Housing is a builder of two types of modular homes, a rambler and a spilt-level. The rambler requires 400 worker-days of carpentry, 10 worker-days of painting and sells for a profit of $3000. The split-level requires 300 worker-days of carpentry, 20 worker-days of painting and sells for a profit of $4000. North America Housing has available 48,000 worker-days of carpentry and 1600 worker-days of painting. North America Housing must also produce at least twice as many ramblers as split-levels. The builder will choose the number of each type of house it builds in order to maximize its profit.(a) Define the variables.(b) Write the system of linear inequalities used in solving the problem.(c) Write an algebraic expression for the objective function.
What will be an ideal response?
| (a) | x = number of ramblers, y = number of split levels |
| (c) | 3000x + 4000y |
You might also like to view...
Find the equation of the axis of symmetry of the parabola.y = -3x2 + 6x - 9
A. x = 6 B. x = 2 C. x = - 1 D. x = 1
Simplify the expression using the quotients-to-powers rule.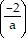
5
A. 
B. 
C. 
D. 
Solve the problem.A satellite dish is in the shape of a parabolic surface. Signals coming from a satellite strike the surface of the dish and are reflected to the focus, where the receiver is located. The satellite dish shown has a diameter of 14 feet and a depth of 3 feet. The parabola is positioned in a rectangular coordinate system with its vertex at the origin. Write an equation in the form of 
for the parabola used to shape the dish. 
A. y =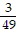 
x2
B. y = 
x2
C. y = 
x2
D. y = 
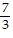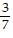x2
Using the factoring method, solve for the roots of the quadratic equation.x(5x + 13) = 6
A. x = 
, x = -3
B. x =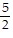 
, x = 3
C. x = 0, x =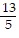 
D. x = 0, x = - 