For a vernier caliper setting of 2.379, what is the vernier graduation that coincides with a main scale graduation?
A. 4
B. 5
C. 7
D. 9
Answer: A
You might also like to view...
The outer electron shell is known as a(an) ________.
A) Unstable shell B) Distant ring C) Valence ring D) None of these
The additives sometimes used in hog rations are dewormers and _____.
Fill in the blank(s) with the appropriate word(s).
What device passes AC interference to ground and blocks DC voltage, and is used to control radio interference?
A) Capacitor B) Transistor C) Coil (inductor) D) Resistor
A classical example of the use of feedback is the phase-locked loop used to demodulate frequency-modulated signals (Figure E.27).
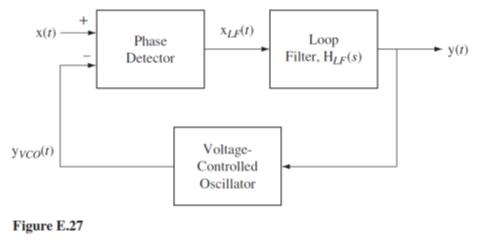
The excitation, x(t) , is a frequency-modulated sinusoid. The phase detector detects the phase difference between the excitation and the signal produced by the voltage-controlled oscillator. The response of the phase detector is a voltage proportional to phase difference. The loop filter filters that voltage. Then the loop filter response controls the frequency of the voltage-controlled oscillator. When the excitation is at a constant frequency and the loop is “locked” the phase difference between the two phase-detector excitation signals is zero. (In an actual phase detector the phase difference is near 90° at lock. But that is not significant in this analysis since that only causes a near 90° phase shift and has no impact on system performance or stability.) As the frequency of the excitation, x (t) , varies, the loop detects the accompanying phase variation and tracks it. The overall response signal, y (t) , is a signal proportional to the frequency of the excitation.
The actual excitation, in a system sense, of this system is not x(t) , but rather the phase of x(t) , ?x(t) , because the phase detector detects differences in phase, not voltage. Let the frequency of x(t) be fx(t) . The relation between phase and frequency can be seen by examining a sinusoid.
Let x(t) = A cos (2? f0t) . The phase of this cosine is 2? f0t and, for a simple sinusoid ( f0 constant), it increases linearly with time. The frequency is f0, the derivative of the phase.
Therefore the relation between phase and frequency for a frequency-modulated signal is
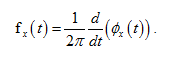
Let the frequency of the excitation be 100 MHz. Let the transfer function of the voltage-controlled oscillator be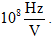 
Let the transfer function of the loop filter be 
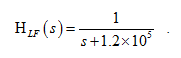Let the transfer function of the phase detector be 1 V/radian. If the frequency of the excitation signal suddenly changes to 100.001MHz, graph the change in the output signal ? y (t) .