Find all points where the function has any relative extrema or saddle points and identify the type of relative extremum.f(x,y) = x3 - 12xy + 8y3
A. Saddle point at (2,1)
B. Relative minimum at (2,1) and saddle point at (0, 0)
C. Relative minimum at (2,1) and relative maximum at (0, 0)
D. Relative maximum at (1, 2)
Answer: B
You might also like to view...
Use Euler's method to approximate the solution. Also find the exact solution. Round your answers to four decimal places.Use Euler's method with h = 0.2 to approximate y(1) given that y' = y and y(0) = 
. Also find the exact value of y(1). 
A. y(1) ? 0.5364; y(1) = 0.5437 B. y(1) ? 0.5184; y(1) = 0.6796 C. y(1) ? 0.6221; y(1) = 0.6796 D. y(1) ? 0.9281; y(1) = 0.8155
Determine whether or not the function is one-to-one.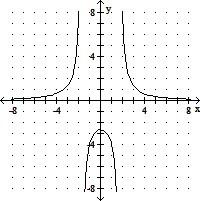
A. No B. Yes
Determine whether the statement is true or false.
?
If f is differentiable, then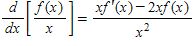 
.
?
A. false B. true
Find decimal notation for the number in percent notation.Only 0.4% of those polled had heard the news.
A. 0.04 B. 0.4 C. 0.004 D. 0.0004