Solve the problem.The supply S and demand D for a certain commodity satisfy the equations S = 25 - 2p(t) + 4p'(t) and 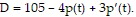 If p(0) = 55, find the equilibrium price p at time t and the long-range equilibrium price.
If p(0) = 55, find the equilibrium price p at time t and the long-range equilibrium price.
A. The equilibrium price p for time t is p(t) = 10e-3t + 20. The long-range equilibrium price  is 20.
is 20.
B. The equilibrium price p for time t is p(t) = 15e-2t + 40. The long-range equilibrium price  is 40.
is 40.
C. The equilibrium price p for time t is p(t) = 15e-2t + 40. The long-range equilibrium price  is 15.
is 15.
D. The equilibrium price p for time t is p(t) = 10e-3t + 20. The long-range equilibrium price 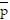 is 10.
is 10.
Answer: B
You might also like to view...
Perform the desired operation. Write the answer in the form a + bi.-2i(-4 + 2i)
A. 4 + 8i B. 8i - 4i2 C. 8i + 4i2 D. -4 + 8i
Use the laws of exponents to simplify each expression using positive exponents only. Assume all variables represent nonzero real numbers.(x-6)-3
A. 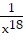
B. x18
C. -x9
D. 
Solve the problem.A contractor needs to know the height of a building to estimate the cost of a job. From a point 96 feet away from the base of the building, the angle of elevation to the top of the building is found to be 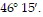 Find the height of the building. Round your answer to the hundredths place.
Find the height of the building. Round your answer to the hundredths place.
A. 98.75 ft B. 103.18 ft C. 100.28 ft D. 104.51 ft
Find an equation for the hyperbola described. Graph the equation.Center at (0, 0); vertex at (0, 2); focus at (0,  )
)
A.  -
- 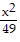 = 1
= 1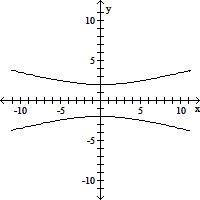
B. 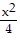 -
-  = 1
= 1
C. 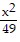 -
- 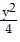 = 1
= 1
D.  -
- 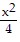 = 1
= 1