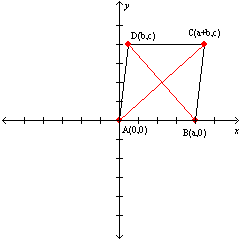
Let a, b, and c represent positive real numbers. Use the figure in which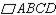 
has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c) to prove the following theorem.“If the diagonals of a parallelogram are equal in length, then the parallelogram is a rectangle.”
What will be an ideal response?
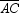and 
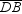are equal in length, then 
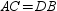. Applying the Distance Formula, 
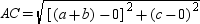so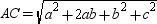 
. Also, 
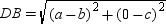so that 
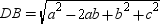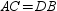
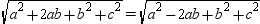
.If , then 
.
Squaring, we have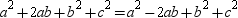 
.
By subtraction of like terms,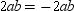 
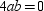
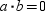
. In turn, 
. Dividing by 4, 
,
But 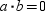only if a = 0 or b = 0.
Because a cannot equal 0 (points A and B would coincide), it is necessary that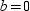 
.
If 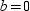, then the vertices of the parallelogram become A(0,0), B(a,0), C(a,c), and D(0,c).
Becuase these vertices lead to the relationship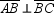 
, ABCD must be a rectangle.
You might also like to view...
Find the slope of the curve for the given value of x.y = x2 + 11x - 15, x = 1
A. slope is -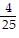 
B. slope is 13
C. slope is -39
D. slope is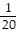 
Add.12 + 31 + 21
A. 55 B. 64 C. 46 D. 37
Ralph has budgeted $175 for entertainment. He uses this money to go out on dates for $35 or to go out with his friends for $15. Which budget line equation represents the situation?
A. 35x - 15y = 180 B. 35x + 15y = 180 C. (3x + 5y) = 180 D. 180 - (35x + 15y)
Find the area of the triangle having the given measurements. Round to the nearest square unit.A = 26°, b = 17 meters, c = 5 meters
A. 38 square meters B. 10 square meters C. 40 square meters D. 19 square meters