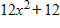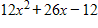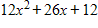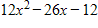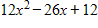Solve the problem.A person's metabolic rate tends to go up after eating a meal and then, after some time has passed, it returns to a resting metabolic rate. This phenomenon is known as the thermic effect of food, and the effect (in kJ/hr) for one individual is F(t) = -10.28 + 175.9te-t/1.3where t is the number of hours that have elapsed since eating a meal. Find the total thermic energy of a meal for the next four hours after a meal by integrating the thermic effect function between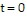 
and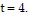 
A. 200.3 kJ
B. 128.4 kJ
C. 186.5 kJ
D. 150.1 kJ
Answer: A
You might also like to view...
Find the mean of the data set: 2, 2, 7, 8, 9, 12, 13, 16 ?
A. ?69 B. 8.625 C. ?9.571 (rounded to 1/1000ths) D. ?1.70 (rounded to 1/100ths) E. ?6.9
Multiply or find the special product.
?
?
A. 
B. 
C. 
D. 
E. 
Find a cofunction with the same value as the given expression.sin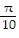
A. cos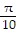 
B. sin 
C. sin 
D. cos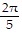 
Solve the problem. Suppose a student plans to drive from his home to New Haven 75 miles on a divided highway and 30 miles on an undivided highway. The speed limit is 70 mph on the divided highway and 50 mph on the undivided highway. Assume the driver drives nonstop. Let T(a) represent the driving time (in hours) if the student drives at a mph above the speed limits. By finding a formula for T(a), determine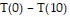 
. What does your result mean in terms of the trip?
A. T(0) - T(10) = 0.23; the trip will take 0.23 hours more by driving at 10 mph over the speed limits than it would take driving at the speed limits. B. T(0) - T(10) = 0.37; the trip will take 0.37 hours less by driving at 10 mph over the speed limits than it would take driving at the speed limits. C. T(0) - T(10) = 0.37; the trip will take 0.37 hours more by driving at 10 mph over the speed limits than it would take driving at the speed limits. D. T(0) - T(10) = 0.23; the trip will take 0.23 hours less by driving at 10 mph over the speed limits than it would take driving at the speed limits.