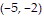Find the maximum and minimum values of the function and the values of x and y for which they occur.G = 6x + 8y, subject to2x + 4y ? 12,2x + y ? 8,0 ? x ? 6,0 ? y ? 4.
A. Maximum: 44 when x = 2 and y = 4; minimum: 30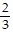 when x = 3
when x = 3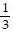 and y = 1
and y = 1
B. Maximum: 30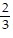 when x = 3
when x = 3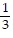 and y = 1
and y = 1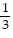 ; minimum: 0 when x = 0 and y = 0
; minimum: 0 when x = 0 and y = 0
C. Maximum: 68 when x = 6 and y = 4; minimum: 0 when x = 0 and y = 0
D. Maximum: 68 when x = 6 and y = 4; minimum: 30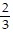 when x = 3
when x = 3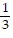 and y = 1
and y = 1
Answer: D
You might also like to view...
Find the midpoint of the segment with the given endpoints. and
and 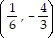
A. 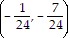
B. 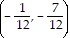
C. 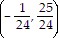
D. 
Solve the application problem.Find three consecutive integers such that the square of the sum of the smaller two is 297 more than the square of the largest.
A. 10, 11, 12 B. 8, 10, 12 C. -10, -9, -8 D. 10, 11, 12, or -10, -9, -8
Find the composite function for the given functions.f ? g for f(x) = 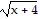 and g(x) = 8x - 8
and g(x) = 8x - 8
A. 8 - 8
- 8
B. 2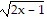
C. 8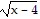
D. 2
Determine the intervals on which the function is increasing, decreasing, and constant.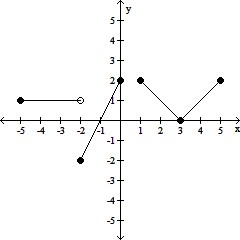
A. Increasing on (-1, 0) and (3, 5); Decreasing on (0, 3); Constant on (-5, -3)
B. Increasing on (-2, 0) and (3, 4); Decreasing on (-5, -2) and (1, 3)
C. Increasing on (1, 3); Decreasing on (-2, 0) and (3, 5); Constant on (2, 5)
D. Increasing on (-2, 0) and (3, 5); Decreasing on (1, 3); Constant on