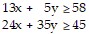Multiply, and then simplify if possible. Assume all variables represent positive real numbers.(5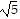
+ 9)2
A. 44 + 90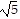
B. 206 - 90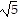
C. 206 + 90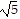
D. 134 + 90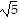
Answer: C
You might also like to view...
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated line.About the line y = -1x =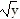 
(solid)
A. 
?
B. 
?
C. 
?
D.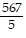 
?
The equation of change for a certain fish population is
.
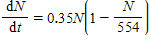
Here N in measured in tons of fish, and t is measured in years. The variable F is the number of tons of fish per year taken by fishing.
?
A: What number of tons of fish per year can be taken by fishing if the population is to be maintained at a level of 428 tons? That is, for what value of F will 428 be an equilibrium solution? Round your answer to two decimal places.B: What will happen to the population if the population is 428 tons and the amount of fish taken by fishing is 41 tons per year?C: Find the equilibrium solutions if 41 tons per year are taken by fishing. Round your answers to two decimal places.
What will be an ideal response?
Provide an appropriate response.Examine the discriminant and find the roots of the equation, rounding to the nearest hundredth if necessary: 12 + 4x - x2 = 0
A. x = -2, 6 B. x = 2.42, -0.42 C. x = 2 + 2.83i, 2 - 2.83i D. x = 2, -6
Set up the linear programming problem.A dietitian needs to purchase food for patients. She can purchase an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. The dietician is bound by the following constraints.? Each ounce of chicken contains 13 grams of protein and 24 grams of carbohydrates.? Each ounce of potatoes contains 5 grams of protein and 35 grams of carbohydrates.? The minimum daily requirements for the patients under the dietitian's care are 45 grams of protein and 58 grams of carbohydrates. Let x = the number of ounces of chicken and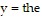 
number of ounces of potatoes purchased per patient. Write a system of inequalities that describes these
constraints.
A. 
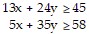
B. 
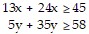
C. 
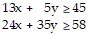
D. 
