Find the first three nonzero terms of the Maclaurin series for the given function and the values of x for which the series converges absolutely.f(x) = cos x - 
A. -4 - x -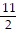 
x2 - ..., -1 < x < 1
B. -4 + 5x +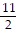 
x2 + ..., -1 < x < 1
C. -4 - 5x +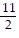 
x2 - ..., -1 < x < 1
D. -4 - 5x -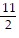 
x2 - ..., -1 < x < 1
Answer: D
You might also like to view...
Use identities to find the indicated value for each angle measure.tan ? =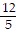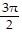 
, ? < ? < 
Find sin(2?).
A.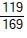 
B. - 
C. - 
D.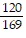 
Simplify the expression. Assume all variables represent nonnegative real numbers.(x2/7)4/5
A. x8/5 B. x38/35 C. x35/8 D. x8/35
Write out the first five terms of the sequence.{sn} =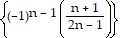 
A. s1= -2, s2= 1, s3=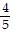 
, s4= - 
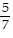, s5=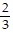 
B. s1= -2, s2= 1, s3= -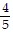 
, s4=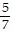 
, s5= -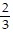 
C. s1= 2, s2= - 1, s3=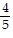 
, s4= - 
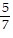, s5=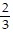 
D. s1= 2, s2= 1, s3=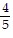 
, s4= 
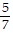, s5=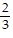 
Factor out the indicated common factor of the expression. Then completely factor the expression.X5/2 - 25x1/2; x1/2
A. x1/2(x5 - 25x) B. x1/2(x - 5)2 C. x1/2(x - 5)(x + 5) D. x1/2(x2 - 25)