Solve the problem.There are 20 bags filled with coins that all look alike. The coins in 19 of the bags are authentic and weigh 10 ounces each. The coins in one of the bags are counterfeit and weigh 11 ounces each. With only one weighing on a scale, how can you determine which bag contains the counterfeit coins?
What will be an ideal response?
Label the bags 1-20 and choose one coin from bag 1, two coins from bag 2, three coins from bag 3, and so on. Weigh all the coins you chose together, a total of 210 coins. If all the coins were authentic, they would would weigh 2100 oz, since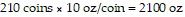 
.
However, 1-20 of the coins are counterfeit, and each (11-oz) counterfeit coin will add an extra ounce to the weight. If the actual weight is 2101, there must be one counterfeit coin, and since one coin was chosen from bag 1, bag 1 must have the counterfeit coins. If the actual weight is 2102, bag 2 must have the counterfeits; if the actual weight is 2103, bag 3 must have the counterfeits, etc. In general: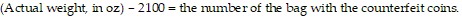
You might also like to view...
Find the apportionment asked for.A small city has 50 police officers to be apportioned among 8 precincts based on the population of each precinct. The populations are given in the following table. 
Find the apportionment for the Seventh Precinct using Adams' method.
A. 4 B. 7 C. 6 D. 5
Solve the problem.The water in a tank weighs 332.03 lb. One cubic foot of water weighs 62.5 lb. How many cubic feet of water are in the tank?
A. 394.53 cubic feet B. 0.18824 cubic feet C. 5.31248 cubic feet D. 20,751.875 cubic feet
Solve the equation for the specified variable.V =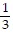 
Bh for h
A. h =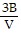 
B. h =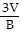 
C. h =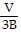 
D. h = 
Determine the function f(x) that has been graphed. The function will be of the form f(x) a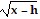
+ k or f(x) = a(x - h)3 + k. Assume a = 1 or a = -1.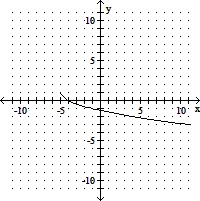
A. f(x) = -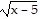
+ 1
B. f(x) = -
+ 1
C. f(x) = -
- 1
D. f(x) = -
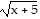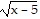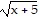- 1