Solve the problem.Five cards are drawn at random from an ordinary deck of 52 cards. In how many ways is it possible to draw two red cards and three black cards?
A. 422,500 ways
B. 1,690,000 ways
C. 1,267,500 ways
D. 845,000 ways
Answer: D
You might also like to view...
Construct a truth table for the statement.(p ? q) ? (~p ? q)
A. 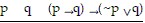
| T | T | T |
F T T
F F F
B.
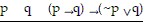
| T | T | T |
F T T
F F T
C.
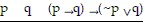
| T | T | T |
F T T
F F T
D.
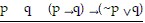
| T | T | F |
F T F
F F F
Provide an appropriate response.Give the signs of the three trigonometric functions of the vector with the endpoint (-3, 5).
A. sine, positive; cosine, negative; tangent, negative B. sine, negative; cosine, positive; tangent, positive C. sine, positive; cosine, positive; tangent, negative D. sine, positive; cosine, negative; tangent, positive
Find the center and radius of the circle.(x - 4)2 + (y + 2)2 = 9
A. Center: (-2, 4); radius: 9 B. Center: (-2, 4); radius: 3 C. Center: (4, -2); radius: 3 D. Center: (4, -2); radius: 9
Write the following as an algebraic expression. Simplify if possible.Subtract 6x + 10 from 4x - 8.
A. -2x - 2 B. 10x + 2 C. 2x + 18 D. -2x - 18