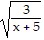Use mathematical induction to prove the statement is true for all positive integers n.1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + n(n + 1) = 
What will be an ideal response?
Answers may vary. Possible answer:
First, we show the statement is true when n = 1.
For n = 1, we get 1 ? 2 = 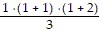
Since 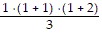 =
= 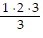 = 1 ? 2, P1 is true and the first condition for the principle of induction is satisfied.
= 1 ? 2, P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
Pk: 1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + k(k + 1) =  is assumed true.
is assumed true.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: 1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + k(k + 1) + (k + 1)(k + 2) = 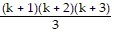
So we assume that 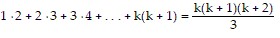 is true and add the next term,
is true and add the next term, 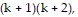 to both sides of the equation.
to both sides of the equation.
1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + k(k + 1) + (k + 1)(k + 2) = 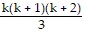 + (k + 1)(k + 2)
+ (k + 1)(k + 2)
1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + k(k + 1) + (k + 1)(k + 2) = 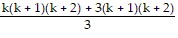
1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + k(k + 1) + (k + 1)(k + 2) = 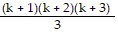
The last equation says that Pk+1 is true if Pk is assumed to be true. Therefore, by the principle of mathematical induction, the statement 1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + n(n + 1) = 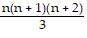 is true for all natural numbers n.
is true for all natural numbers n.
You might also like to view...
Perform the indicated operation(s). Where possible, reduce the answer to lowest terms. ÷
÷ 
A. 0
B. 
C. 
D. - 
Find the value of x:
8 2x Ä = ÄÄ x 16 a. 8.0 b. 11.3 c. 16 d. 19.8 e. 23.9
Simplify

The function f is one-to-one. Find its inverse.f(x) = 3x2 - 5, x ? 0
A. f-1(x) = - 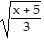
B. f-1(x) = 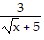
C. f-1(x) = 
D. f-1(x) =