Give the two-symbol classification of the border pattern.Z Z Z Z Z Z
A. 11
B. 12
C. 1g
D. 1m
Answer: B
You might also like to view...
Solve the problem.Alayna gets reimbursed by her company for travel expenses. Her company pays $0.30 per mile when employees use their own vehicle, which she did. She drove 482 miles and spent $50.00 on gas. She spent three nights in a hotel at $97.20 per night and spent $93.93 on food. Write a numerical expression that describes her total expenses, then find the total expenses.
A. 482 + 50.00 + 3(97.20) + 93.93 =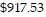 
B. 0.30(482) + 50.00 + 3(97.20) + 93.93 =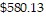 
C. 0.30(482) + 50.00 + 97.20 + 93.93 =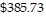 
D. 0.30(482) + 3(97.20) + 93.93 =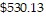 
Find the Jacobian for the given transformation.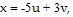
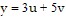
A. 16 B. 34 C. -34 D. -16
Estimate and find the actual difference expressed as a mixed number in simplest form.6
- 4
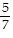
A. Estimate: 2; Actual: 2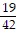
B. Estimate: 2; Actual: 1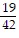
C. Estimate: 1; Actual: 2
D. Estimate: 1; Actual: 1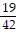
Solve the problem.During rush hours, substantial traffic congestion is encountered at the intersections shown inthe figure. The arrows indicate one-way streets. As the figure shows, 200 cars per hour come down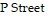 
to intersection A, and 800 cars per hour come down 
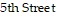to intersection A. x of these cars leave A on 
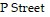and w cars leave A on 
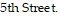-4.0px;" /> 800 in 600 out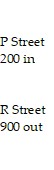 
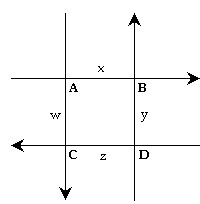
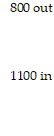200 out 400 in 5th Street 6th StreetThe number of cars entering intersection A must equal the number leaving, so that 
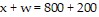or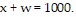 
By writing an equation representing the traffic entering and leaving each of the intersections A, B, C, and D, obtain a system of four equations. Solve the system using w as the parameter and use your answer to determine the largest and smallest possible values for the number of cars leaving intersection D on R Street.
A. 1000; 100
B. 1100; 0
C. 1000; 0
D. 1100; 100