Solve the linear programming problem.Mrs. White wants to crochet beach hats and baby afghans for a church fund-raising bazaar. She needs 7 hours to make a hat and 2 hours to make an afghan and she has 53 hours available. She wants to make no more than 14 items and no more than 11 afghans. The bazaar will sell the hats for $13 each and the afghans for $7 each. How many of each should she make to maximize the income for the bazaar? What is the maximum income?
A. 7 hats, 7 afghans, $140
B. 5 hats, 9 afghans, $128
C. 9 hats, 5 afghans, $152
D. 11 hats, 3 afghans, $164
Answer: B
You might also like to view...
Find the standard form of the polynomial function of smallest degree with real coefficients satisfying the given conditions. f(0) = 39, -3 and 3 - 2i are roots
A. f(x) = x3 - 3x2 + 5x - 52 B. f(x) = x3 - x2 - 5x + 39 C. f(x) = x3 - x2 + 11x + 39 D. f(x) = x3 - 3x2 - 5x + 39
Provide an appropriate response.Identify the greatest common factor (GCF) of 2x2 + 4x.
A. 2 B. 4x C. x D. 2x
Match the correct graph to the given function. y = (x - 6)2 - 1
A. 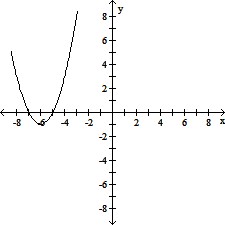
B. 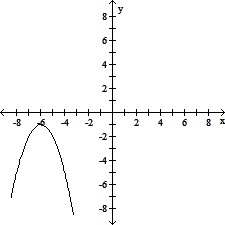
C. 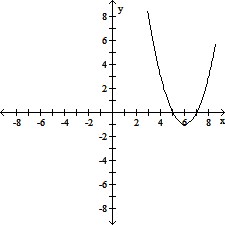
D. 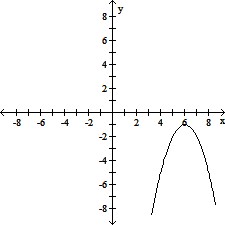
Find the minimum and maximum values of the objective function and where it occurs, subject to the indicated constraints.
Objective function: z = 3x + 4y
Constraints: 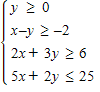
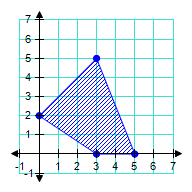
A. minimum = 8 at (0, 2); maximum = 29 at (3, 5) B. minimum = -11 at (3, 5); maximum = 15 at (5, 0) C. minimum = 8 at (0, 2); maximum = 27 at (3, 5) D. minimum = 0 at (0, 0); maximum = 29 at (3, 5) E. minimum = 9 at (3, 0); maximum = 15 at (5, 0)