Solve the problem.A truck rental company rents a moving truck one day by charging $39 plus $0.09 per mile. Write a linear equation that relates the cost C, in dollars, of renting the truck to the number x of miles driven. What is the cost of renting the truck if the truck is driven 120 miles?
A. C(x) = 0.09x + 39; $40.08
B. C(x) = 0.09x - 39; -$28.20
C. C(x) = 0.09x + 39; $49.80
D. C(x) = 39x + 0.09; $4,680.09
Answer: C
You might also like to view...
The critical value corresponding to a level of significance of? = 0.01 .
The probability density function of X is 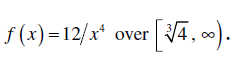
Compute the following quantity.
Divide. Express the quotient in lowest terms.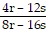 ÷
÷ 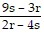
A. 3
B. - 3
C. - 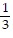
D. - 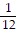
Provide an appropriate response.Assume that the events A1, A2, . . . , An are mutually exclusive events whose union is the sample space, and that B is an event that has occurred. Use Bayes' theorem to write an equation for 
What will be an ideal response?
Rewrite the objective function into a maximization function.Minimizew = y1 + 3y2 + y3 + 4y4subject to:y1 + y2 + y3 + y4 ? 31 2y1 + 2y2 + y3 + 2y4 ? 58 y1 ? 0, y2 ? 0, y3 ? 0, y4 ? 0
A. Maximize z = -x1 - x2 - x3 - x4 ? -31 B. Maximize z = -2x1 - 2x2 - x3 - 3x4 ? -58 C. Maximize z = x1 + 3x2 + x3 + 4x4 - x5 D. Maximize z = -x1 - 3x2 - x3 - 4x4