Verify that each equation is an identity.cos(3x) = cos3 x - 3 sin2 x cos x
What will be an ideal response?
cos(3x) = cos(2x + x) = cos(2x) cos x - sin(2x) sin x = (cos2 x - sin2 x) cos x - 2 sin x cos x sin x =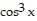 
- sin2 x cos x - 2 sin2 x cos x = cos3 x - 3 sin2 x cos x.
You might also like to view...
Write a system of linear equations in three variables, and then use matrices to solve the system.Ron attends a cocktail party (with his graphing calculator in his pocket). He wants to limit his food intake to 103 g protein, 93 g fat, and 135 g carbohydrate. According to the health conscious hostess, the marinated mushroom caps have 3 g protein, 5 g fat, and 9 g carbohydrate; the spicy meatballs have 14 g protein, 7 g fat, and 15 g carbohydrate; and the deviled eggs have 13 g protein, 15 g fat, and 6 g carbohydrate. How many of each snack can he eat to obtain his goal?
A. 7 mushrooms; 4 meatballs; 2 eggs B. 2 mushrooms; 7 meatballs; 4 eggs C. 4 mushrooms; 2 meatballs; 7 eggs D. 8 mushrooms; 5 meatballs; 3 eggs
Perform the matrix operation.Given C =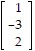 
and D = 
, find C - 4D.
A. 
B. 
C. 
D. 
Evaluate the expression.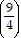
3
A.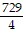 
B. 3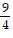
C. 
D. 
Find the least common multiple of the numbers.210 and 360
A. 75,600 B. 10,800 C. 6300 D. 2520