Use mathematical induction to prove that the statement is true for every positive integer n.(22)n = 22n
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. The left-hand side becomes (22)(1) = 811 = 81 . The right-hand side becomes 34(1) = 34 = 81. Thus, the statement is true for n = 1.
b). Assume the statement is true for n = k:
(34)k= 34k
Multiply both sides by 34:
34(34)k = 34k?34
Using the product rule for exponents and the distributive property,
(34)(k+1) = 34k+4 = 34(k+1)
The statement is true for n = k + 1 as long as it is true for n = k. furthermore, it is true for n = 1. Thus, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem.You are planning on taking some classes at the local art studio this summer. The cost is $35 per class attended and a one-time supply fee of $30. You have $390 to spend on summer art classes. How many art classes can you attend? Round to the nearest whole number.
A. 12 classes B. 10 classes C. 11 classes D. 9 classes
Add or subtract.(3 + 4i) - (-8 + i)
A. 11 + 3i B. 11 - 3i C. -11 - 3i D. -5 + 5i
Multiply.(4a + 11c)(4a - 11c)
A. 4a2 - 11c2 B. 16a2 + 88ac - 121c2 C. 16a2 - 121c2 D. 16a2 - 88ac - 121c2
Solve the equation.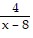 =
= 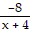
A. 8, -4
B. - 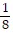 ,
, 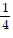
C. 4
D. - 20