Solve the problem.An open-top box is to be constructed from a 9 cm by 11 cm piece of cardboard by cutting out squares from each corner and folding up the sides as shown in the figure. Find a polynomial that represents the area of the bottom of the box in the accompanying figure. Find a polynomial that represents the volume of the box. 
A. Area of bottom: 4x2 - 38x + 90, Volume: 4x3 - 38x2 + 90x
B. Area of bottom: 4x2 - 40x + 99, Volume: 4x3 - 40x2 + 99x
C. Area of bottom: 4x2 + 40x + 99, Volume: 4x3 + 40x2 + 99x
D. Area of bottom: 4x2 - 38x - 90, Volume: 4x3 - 38x2 - 90x
Answer: B
You might also like to view...
Find the x- and y-intercepts. If no x-intercepts exist, state so.y = x2 - 3x + 5
A. No x-intercepts, (0, 5)
B.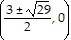 
, (0, -5)
C. No x-intercepts, (0, -5)
D.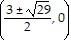 
, (0, 5)
Factor completely. If unfactorable, indicate that the polynomial is prime.27k4t2 - 75k2t4
A. 3(3k2t + 5kt2)2 B. 3(3k2t + 5kt2)(3k2t - 5kt2) C. 3k2t2(3k - 5t)2 D. 3k2t2(3k + 5t)(3k - 5t)
Solve the problem.The cost of producing t units is C = 3t2 + 9t, and the revenue generated from sales is R = 4t2 + t. Determine the number of units to be sold in order to generate a profit.
A. t > 10 B. t > 8 C. t > 0 D. t > 9
Find the indicated sum.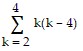
A. -4 B. -10 C. 6 D. -7