Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the maximum profit occurs for the given objective function.?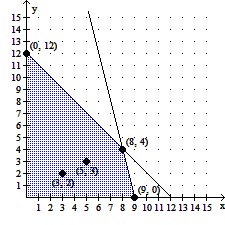
P = 5x + y
A. Max P = 44 at x = 8 and y = 4, at x = 0 and y = 12, and at every point on the line segment joining the preceding two points.
B. Max P = 44 at x = 8 and y = 4
C. Max P = 45 at x = 9 and y = 0
D. Max P = 45 at x = 9 and y = 0, at x = 8 and y = 4, and at every point on the line segment joining the preceding two points.
Answer: C
You might also like to view...
Given the graph of f, find any values of x at which f ' is not defined.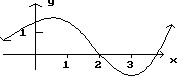
A. x = 2 B. x = 1, 2, 3 C. x = 1, 3 D. Defined for all values of x
Evaluate. Assume u > 0 when ln u appears.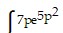 
dp
A.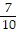 
e5p2+ C
B. 7e5p2 + C
C. -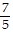 
e5p2 + C
D. -7e5p2 + C
Solve the problem.Use the trigonometric identity tan 2x = 
to find Dxtan 2x.
A. 2 sec2x(1 - tan2x) B. 2 sec2x(1 + tan2x) C. 2 sec2x tan2x D. 2 tan2x + tan3x
Solve the problem.Find the polynomial that represents the area of the rectangle below (Hint: Area = Length ? Width.)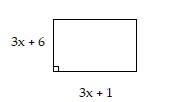
A. 9x2 + 21x + 6 B. 9x2 + 6 C. 6x2 + 9 D. 6x2 + 21x + 9