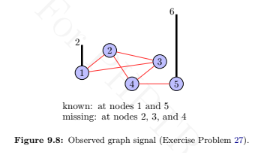
This problem demonstrates the use of Laplacian quadratic form for interpolation on graphs. Consider an observed graph signal, shown in Figure 9.8, where signal values at nodes 2, 3, and 4 are missing. The aim of interpolation is to fill in the missing values. One criteria for estimating the missing values is to minimize the squared sum of the differences in signal values between the neighboring vertices, which is nothing but the quadratic form of the graph Laplacian. Therefore, the interpolation problem can be written as
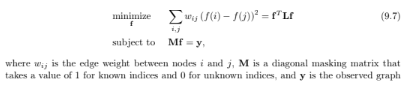
signal with zeros at missing indices. For example, if the values at nodes 2, 3, and 4 are
missing, the masking matrix is
M = diag {1,0,0,0,1} and the observed graph signal can be
written as y = [2, 0, 0, 0, 6] T. Find the missing values in the observed graph signal by solving
the above optimization problem. Hint: Use the method of Lagrange multipliers.

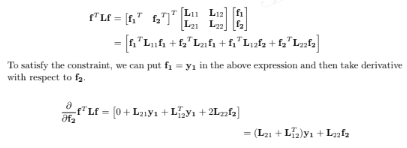

You might also like to view...
Imagine that you saw a Usenet posting with something particularly funny in it and saved the posting to a file. How would you incorporate this file into your own buffer? What if you wanted to use only a couple of paragraphs from the posting? How would you add > to the beginning of each included line?
What will be an ideal response?
A _____________ device is a wireless device that employees connect and use without authorization or verified configurations.
Fill in the blank(s) with the appropriate word(s).
To update records in a table, use the UPDATE, SET, and WHERE keywords with the mysql_query() function.
Answer the following statement true (T) or false (F)
Where can’t you see errors?
a) The line where the error occurred b) The Error List window c) The Solution window d) The Command Prompt window