Provide an appropriate response.Derive the equations x = x0 +  (1 - e-kt)cos ?, y = y0 +
(1 - e-kt)cos ?, y = y0 +  (1 - e-kt)sin ? +
(1 - e-kt)sin ? +  (1 - kt - e-kt)by solving the following initial value problem for a vector r in the plane. Differential equation:
(1 - kt - e-kt)by solving the following initial value problem for a vector r in the plane. Differential equation:  = -gj - kv = -gj - k
= -gj - kv = -gj - k Initial
Initial
conditions: r(0) = x0i + y0j  (0) = v0 = (v0cos ?)i + (v0sin ?)jThe drag coefficient k is a positive constant representing resistance due to air density, v0 and ? are the projectile's initial speed and launch angle, and g is the acceleration of gravity.
(0) = v0 = (v0cos ?)i + (v0sin ?)jThe drag coefficient k is a positive constant representing resistance due to air density, v0 and ? are the projectile's initial speed and launch angle, and g is the acceleration of gravity.
What will be an ideal response?
Problem is separable.
x-coordinate:
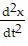 =
= 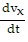 = -kvx or
= -kvx or 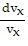 = -k dt. Integrate to get ln
= -k dt. Integrate to get ln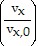 = -kt or
= -kt or
vx = vx,0e-kt
Next, x = 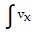 dt =
dt = 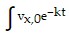 dt = -
dt = - 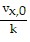 e-kt + C
e-kt + C
At t = 0, x(0) = x0 = - 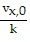 + C or C = x0 +
+ C or C = x0 + 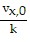
Thus, x = x0 + 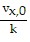 (1 - e-kt). Also, vx,0 = v0cos ?, so
(1 - e-kt). Also, vx,0 = v0cos ?, so
x = x0 + 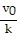 (1 - e-kt)cos ?.
(1 - e-kt)cos ?.
y-coordinate: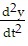 =
= 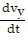 = - g - kvy. Let w =
= - g - kvy. Let w = 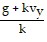 , then
, then 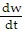 =
= 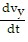 . Make substitutions to get:
. Make substitutions to get: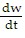 = - kw or
= - kw or 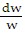 = -k dt. Integrate to get: ln
= -k dt. Integrate to get: ln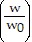 = -kt or w = w0e-kt.
= -kt or w = w0e-kt.
Replace w:
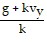 =
= 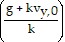 e-kt. Solve for vy to get vy =
e-kt. Solve for vy to get vy = 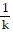 (g + kvy,0)e-kt -
(g + kvy,0)e-kt - 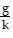 .
.
Finally, y = 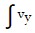 dt =
dt = 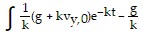 dt = -
dt = - 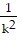 (g + kvy,0)e-kt -
(g + kvy,0)e-kt - 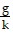 t + C.
t + C.
At t = 0, y = y0 = - 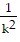 (g + kvy,0) + C or C = y0 +
(g + kvy,0) + C or C = y0 + 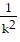 (g + kvy,0). Thus,
(g + kvy,0). Thus,
y = y0 - 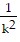 (g + kvy,0)e-kt -
(g + kvy,0)e-kt - 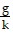 t +
t + 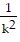 (g + kvy,0)
(g + kvy,0)
= y0 + 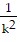 (g + kvy,0)(1 - e-kt) -
(g + kvy,0)(1 - e-kt) - 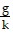 t
t
Also, vy,0 = v0sin ?. Substituting and rearranging:
y = y0 + 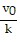 (1 - e-kt)sin ? +
(1 - e-kt)sin ? + 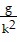 (1 - kt - e-kt)
(1 - kt - e-kt)
You might also like to view...
Write the numeral as a Babylonian numeral.122
A. ![]()
![]()
![]()
![]()
B.
C.
D.
Suppose that y is inversely proportional to x. Use the given information to find the constant of proportionality k. Then use y = 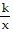 to find y for the given value of x.y = 2.5 when x = 5;
to find y for the given value of x.y = 2.5 when x = 5; Find y given x = 16.
Find y given x = 16.
A. k = 5; y = 
B. k = 0.5; y = 8
C. k = 12.5; y = 
D. k = 2.5; y = 
Solve the problem.Write 0.624 as a fraction.
A. 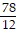
B. 
C. 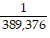
D. 
Solve the inequality analytically, writing the solution set in interval notation.-30 < -5x ? -10
A. [2, 6] B. (2, 6) C. (-6, -2] D. [2, 6)