State the domain and range of the one-to-one functions f and f-1.f(x) =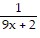 
A. f(x): domain (-?, ?), range (-?, ?);
f-1(x): domain (-?, ?), range (-?, ?)
B. f(x): domain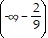 
? 
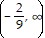, range (-?, 0) ? (0, ?);
f-1(x): range (-?, 0) ? (0, ?), range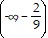 
? 
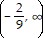
C. f(x): domain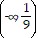 
? 
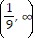, range 
? 
;
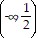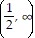f-1(x): domain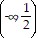 
? 
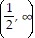, range 
? 
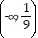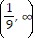
D. f(x): domain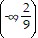 
? 
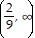, range (-?, -2) ? (-2, ?);
f-1(x): domain (-?, -2) ? (-2, ?), range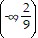 
? 
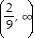
Answer: B
You might also like to view...
Solve.Two airplanes leave an airport at the same time, one going northwest at 405 mph and the other going east at 326 mph. How far apart are the planes after 3 hours (to the nearest mile)?
A. 1618 mi B. 1730 mi C. 2028 mi D. 676 mi
Solve the problem.The total production cost of printing a commemorative booklet for your outdoor group is a flat fee of $500 for typesetting plus 35 cents per copy. Let p represent the total production cost and x represent the number of copies printed. If you decide to sell the booklets for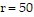 
cents per copy, how many will need to be sold to break even? That is, for what value of x is the total cost of production p equal to the total amount of revenue r? Round to the nearest whole number.
A. 510 booklets B. 3333 booklets C. 588 booklets D. 490 booklets
Solve the problem.A formula for calculating the distance, d, one can see from an airplane to the horizon on a clear day is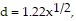 
where x is the altitude of the plane in feet and d is given in miles. How far can one see in a plane flying at 20,000 feet? Round your answer to the nearest tenth mile, if necessary.
A. 12,200 mi B. 172.5 mi C. 1220 mi D. 156.2 mi
Indicate whether the graph of the equation is a circle, an ellipse, a hyperbola, or a parabola. Then graph the conic section.7x2 = 175 + 7y2
A. parabola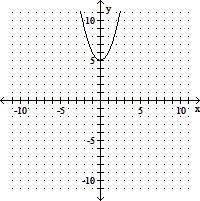
B. hyperbola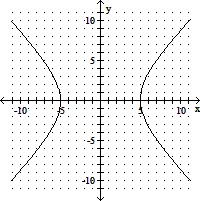
C. circle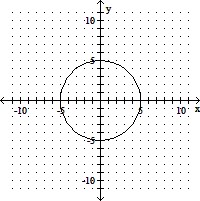
D. ellipse