Solve the problem.If f(x) is a differentiable function and f'(c) = 0 at an interior point c of f's domain, and if 
for all x in the domain, must f have a local minimum at 
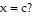Explain.
What will be an ideal response?
Yes. The point x = c is either a local maximum, a local minimum, or an inflection point. But, since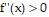 
for all x in the domain, there are no inflection points and the curve is everywhere concave up and thus cannot have a local maximum. Hence, there is a local minimum at x = c.
You might also like to view...
Provide an appropriate response. Solve the given problem: A gear measures 8 cm across. It turns another gear 3.4 cm across. If the larger gear has a speed of 45 revolutions per minute (rpm), what is the rpm of the smaller gear?
A. 0.6 rpm B. 106 rpm C. 19 rpm D. 360 rpm
Find the direction angle ? for the given vector. Let 0° ? ? < 360° and round ? to the nearest tenth when appropriate.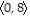
A. 270° B. 45° C. 116° D. 90°
Simplify.
A. 40
B. 30
C. 
D. 10
Graph the function by starting with the graph of the basic function and then using the techniques of shifting, compressing, stretching, and/or reflecting.f(x) =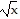 
+ 3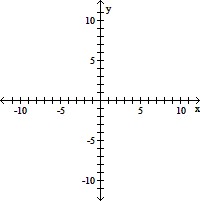
A.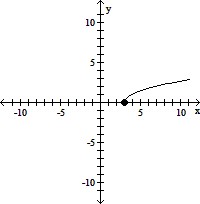 
B. 
C. 
D. 