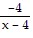Solve the problem.The population of one town is modeled by the function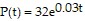 
, and the population of a second town is modeled by the function 
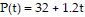. In each case, t is the number of years from the present, and P(t) is given in thousands of people. In how many years is the population of the first town predicted to be twice as large as the population of the second town? (Round to the nearest tenth of a year.)
A. 24.7 years
B. 16.2 years
C. 61.7 years
D. 63.8 years
Answer: D
You might also like to view...
Express as a single logarithm and, if possible, simplify.log5 8 + log5 7
A. log10 56 B. log10 15 C. log5 15 D. log5 56
Solve the problem.The following points form a quadratic relationship: (1, 5.0), (2, 4.4), (3, 4.3), (4, 4.2), (5, 4.6), (6, 4.8), (7, 5.4), (8, 6.2) . The x-coordinates are the years a particular company has been in operation and the y-coordinates are the profit, in millions, for that year. Find the quadratic function that models the profit in millions as a function of x, the number of years of operation. Round to three decimal places.
A. y = - 0.003x2 + 0.145x - 0.892 B. y = 0.101x2 - 0.723x + 5.552 C. y = 0.099x2 + 1.254x - 3.512 D. y = 0.203x2 - 0.945x + 7.098
Graph the function.f(x) = log1/4(x + 2)
A. 
B.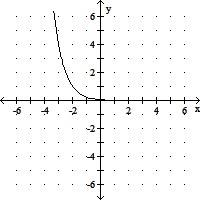 
C.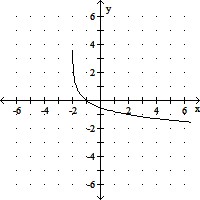 
D.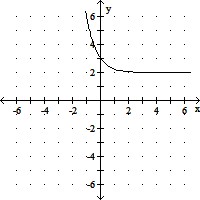 
Write the partial fraction decomposition of the rational expression.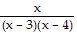
A.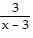 
+ 
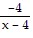
B.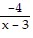 
+ 
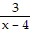
C.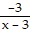 
+ 
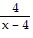
D.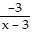 
+ 