Solve the problem.The volume V (in cubic inches) of a cylindrical pipe with length 12 inches is given by V(r) = 12?r2, where r is the radius of the piston (in inches). If the radius is increasing with time t (in minutes) according to the formula r(t) = 
t2, t ? 0, find the volume V of the pipe as a function of the time t.
What will be an ideal response?
V(t) =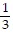 
?t4
You might also like to view...
What is the maximum value of 
? Restrict your attention to the horizontal span of 0 to 20. Round your answer to two decimal places.
?
A. 1.30 B. 4.58 C. 0.07 D. 7.66
Divide. Express the quotient in lowest terms.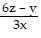
÷ 
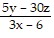
A.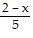 
B.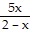 
C.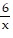 
D.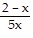 
Solve the problem.If a rocket is propelled upward from ground level, its height in meters after t seconds is given by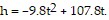 
During what interval of time will the rocket be higher than 294 m?
A. 6 < t < 10 B. 5 < t < 6 C. 0 < t < 5 D. 10 < t < 11
Approximate the area under the curve and above the x-axis using n rectangles. Let the height of each rectangle be given by the value of the function at the right side of the rectangle.f(x) = 2x2 + x + 3 from x = -2 to x = 1; n = 3
A. 25 B. 13 C. 17 D. 21