Solve the problem.A drug is injected into a patient and the concentration of the drug is monitored. The drug's concentration, C(t), in milligrams after t hours is modeled by C(t) =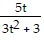 
.What is the end behavior of this function? Describe what this means in practical terms.
A. as x ? ?, C(x) ? 0; 0 is the final amount, in milligrams, of the drug that will be left in the patient's bloodstream.
B. as x ? ?, C(x) ? 1.67; After 1.67 hours, the concentration of the drug is at its greatest.
C. as x ? ?, C(x) ? 0.83; After 0.83 hours, the concentration of the drug is at its greatest.
D. as x ? ?, C(x) ? 1.67; 1.67 is the final amount, in milligrams, of the drug that will be left in the patient's bloodstream.
Answer: A
You might also like to view...
Evaluate the expression by hand.24011/4
A. 196 B. 16,807 C. 28 D. 7
Solve the problem.Jane wants to buy a photocopier. The salesperson has the following information on 3 models. If all 3 are used, a specific job can be done in 50 minutes. If copier A operates for 20 minutes and copier B for 50 minutes, one-half the job is finished. If copier B operates for 30 minutes and copier C for 80 minutes, three-fifths of the job is done. Which is the fastest copier, and how long does it take for this copier to finish the whole job?
A. A is fastest; 120 minutes B. C is fastest; 100 minutes C. B is fastest; 100 minutes D. C is fastest; 120 minutes
Solve the equation.log (5) - log x = log (x - 4)
A. x = 5, x = -1
B. x = -1
C. x = 5
D. x =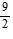 
Assignment- 3
A. X is a discrete random variable. The table below defines a probability distribution for X.
1) What is P (X < 2)? 2) What is P (X > 2)? 3) What is P (2 < X < 5)?
x | P(X=x) |
1 | 0.09 |
2 | 0.03 |
3 | 0.52 |
4 | 0.24 |
5 | 0.12 |
B. Steph makes 90% of the free-throws she attempts. She is going to shoot 3 free-throws. Assume that the results of free-throws are independent from each other. Find the probability that she makes exactly 2 of the 3 free-throws.
C. A large group of students took a test in Physics and the final grades have a mean of 70 and a standard deviation of 10. If we can approximate the distribution of these grades by a normal distribution, what percent of the students should get grades greater than 60?
D. A set of laptop prices are normally distributed with a mean of 750 dollars and a standard deviation of 60 dollars. What proportion of laptop prices are between 624 dollars and 768 dollars?