Solve the problem.The market research department for a drug store chain arrived at the demand table below, where y is the number of bottles of multivitamins purchased per month (in thousands) at x dollars per bottle.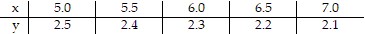 I)Find a demand equation using the method of least squares.II)If each bottle of multivitamins costs the drug store chain $4, how should it be priced to achieve a maximum monthly profit? [Hint: Use the result from I) with
I)Find a demand equation using the method of least squares.II)If each bottle of multivitamins costs the drug store chain $4, how should it be priced to achieve a maximum monthly profit? [Hint: Use the result from I) with 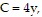
 and
and
src="https://sciemce.com/media/4/ppg__tett0602191629__f1q55g4.jpg" alt="" style="vertical-align: -4.0px;" />
A.
I) y = 0.20x + 3.50
II) $10.75
B. I) y = 0.20x - 3.50
II) $10.75
C. I) y = -0.20x - 3.50
II) $10.75
D. I) y = -0.20x + 3.50
II) $10.75
Answer: D
Mathematics
src="https://sciemce.com/media/4/ppg__tett0602191629__f1q55g4.jpg" alt="" style="vertical-align: -4.0px;" />
A.
| I) | y = 0.20x + 3.50 |
| II) | $10.75 |
B.
| I) | y = 0.20x - 3.50 |
| II) | $10.75 |
C.
| I) | y = -0.20x - 3.50 |
| II) | $10.75 |
D.
| I) | y = -0.20x + 3.50 |
| II) | $10.75 |
Answer: D
You might also like to view...
Express the integrand as a sum of partial fractions and evaluate the integral.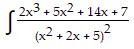 dx
dx
A. - 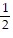 tan-1
tan-1 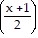 -
- 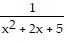 + C
+ C
B. ln 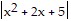 -
- 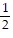 tan-1
tan-1 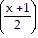 + C
+ C
C. ln 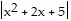 -
- 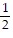 tan-1
tan-1 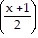 -
- 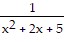 + C
+ C
D. ln 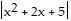 -
- 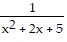 + C
+ C
Solve the problem.A construction company buys a truck for $48,000. The truck is expected to last 16 years, at which time it will be worth $3200. Write a function v(x) that describes the value of the truck at any time during its lifetime. Be sure to state the domain of the function.
A. v(x) = 48 ,000 - 2500t, with domain 0 ? t ? 16 B. v(x) = 48 ,000 - 2300t, with domain 0 ? t ? 16 C. v(x) = 48 ,000 + 2800t, with domain 0 ? t ? 16 D. v(x) = 48 ,000 - 2800t, with domain 0 ? t ? 16
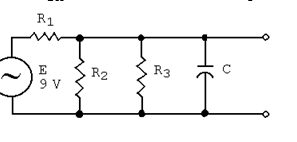
In the circuit below, R1 = 3.3 Kê, R2 = 5.6 Kê, R3 = 4.7 Kê, and C = 846 pF. Find VO and RN of an equivalent Norton circuit.
a. VO = 15.0 V, RN = 4.7 Kê
b. VO = 8.5 V, RN = 5.86 Kê
c. VO = 7.5 V, RN = 2.56 Kê
d. VO = 6.5 V, RN = 3.3 Kê
e. VO = 3.9 V, RN = 1.4 Kê
Determine whether the equation has no solution, one solution, or infinitely many solutions.5x = 6(x + 4) - x
A. One solution B. Infinitely many solutions C. No solutions