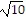Compare the right-hand and left-hand derivatives to determine whether or not the function is differentiable at the point whose coordinates are given.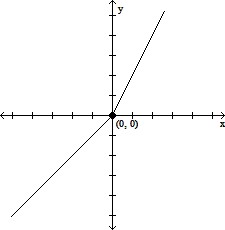 y = xy = 2x
y = xy = 2x
A. Since limx?0+ f '(x) = -2 while limx?0- f '(x) = -1, f(x) is not differentiable at x = 0.
B. Since limx?0+ f '(x) = 2 while limx?0- f '(x) = 1, f(x) is not differentiable at x = 0.
C. Since limx?0+ f '(x) = 1 while limx?0- f '(x) = 2, f(x) is not differentiable at x = 0.
D. Since limx?0+ f '(x) = 1 while limx?0- f '(x) = 1, f(x) is differentiable at x = 0.
Answer: B
You might also like to view...
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary.2x + 5y = -7-6x - 15y = 21
A. {(-1, -1)}
B. ?
C. 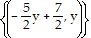
D. 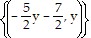
Graph the function. Describe its position relative to the graph of the indicated basic function.f(x) = 5 - 1-x; relative to f(x) = 1x
A. Reflected across y-axis;
reflected across x-axis;
moved up 5 unit(s)
B. Reflected across y-axis;
reflected across x-axis;
moved down 5 unit(s)
C. Moved up 5 unit(s);
reflected across, y-axis;
reflected across x-axis;
D. Moved up 5 unit(s);
reflected across, y-axis;
reflected across x-axis;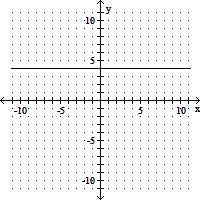
Write the vector v in the form ai + bj, given its magnitude 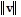 and the angle ? it makes with the positive x-axis.
and the angle ? it makes with the positive x-axis.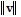 = 3, ? = 60°
= 3, ? = 60°
A. v = - 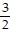 i -
i - 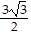 j
j
B. v =  i +
i +  j
j
C. v = 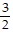 i +
i + 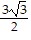 j
j
D. v =  i +
i + 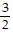 j
j
Solve the problem.If v = 6i + 8j, find 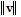 .
.
A. 14
B. 100
C. 10
D.