Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.1 ? 4 + 2 ? 4 + 3 ? 4 + . . . + 4n = 
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 4 =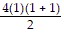 
= 4.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
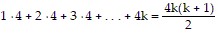is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
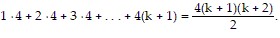
So we assume that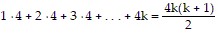 
is true and add the next term, 
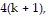to both sides of the equation.
1 ? 4 + 2 ? 4 + 3 ? 4 + . . . + 4k + 4(k + 1) =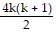 
+ 4(k + 1)
= 
= 
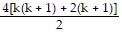
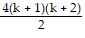
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Using the Divergence Theorem, find the outward flux of F across the boundary of the region D.F = sin yi + xzj + 4zk ; D: the thick sphere 1 ? x2 + y2 + z2 ? 4
A. 
?
B. 112?
C. 32?
D.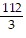 
?
Solve the problem.In the past, Michael had the following success shooting free throws after being fouled.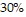 
of the time he got 0 points, 
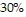of the time he got 1 point, and 
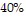of the time 2 points. Use the following set of random digits to simulate 100 free throws. Begin at the top of the first column and move down that column
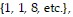then start at
the top of the second column and move down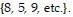 
Use the following: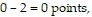 
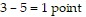and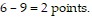 
Estimate the probability that on a given occasion, Michael will score 2 points after being fouled. 
A.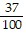 
B.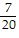 
C.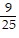 
D.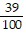 
Use the figure below to answer the following question(s).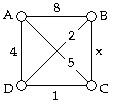
The nearest-neighbor tour with starting vertex A is A, B, C, D, A
A. only if 1 ? x ? 8. B. only if 2 < x < 8. C. only if x < 5. D. only if x = 1. E. regardless of the value of x.
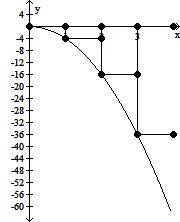
Graph the function f(x) over the given interval. Partition the interval into 4 subintervals of equal length. Then add to your sketch the rectangles associated with the Riemann sum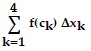 
, using the indicated point in the kth subinterval for ck.f(x) = -4x2, [0, 4], left-hand endpoint
A.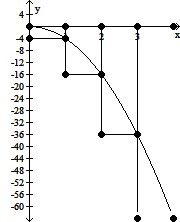 
B. 
C.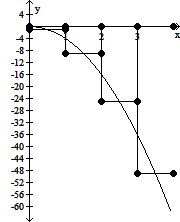 
D. 