Use Lagrange Multipliers to solve the given problem.
?
Find the maximum value of 
subject to 
.
?
A. 
B. 
C. 
D. 
E. 
Answer: B
You might also like to view...
Set up an integral for the length of the curve.x = 7 tan y, 0 ? y ? 
A.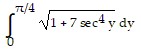 
B.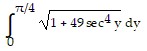 
C.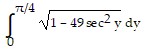 
D.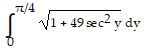 
Solve the problem.An electron beam is deflected in a back-and-forth pattern by a time-periodic voltage, V(t), according to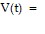
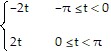where t = 0 marks a reference point in time that is not necessarily the beginning of oscillation.Find ao (if it is not zero), two nonzero cosine terms (if they exist), and two nonzero sine terms (if they exist) of the Fourier series for the time-dependent voltage.
A. V(t) =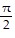 
- 
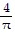
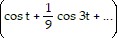
B. V(t) = ? -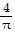 
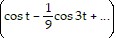
C. V(t) =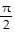 
- 
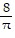
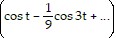
D. V(t) = ? -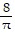 
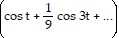
Factor completely, or state that the polynomial is prime.18y2 + 42y + 20
A. 2(10y + 2)(y + 5) B. 2(3y + 1)(3y + 10) C. prime D. 2(3y + 2)(3y + 5)
For what values of does the curve have maximum and minimum points for the given function 
?
Select the correct answer.
a. For 
a parabola whose vertex (0, 2), is the absolute maximum.
For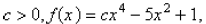 
opens downward with one minimum points.
For c < 0, the graph opens upward, and has an absolute maximum at x=0 and no local minimum.
b. For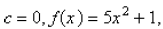 
a parabola whose vertex (0, 2) is the absolute maximum.
For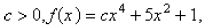 
opens upward with two minimum points.
For c < 0, the graph opens downward, and has an absolute minimum at x=0 and no local minimum.
c. For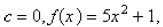 
a parabola whose vertex (0, 3), is the absolute maximum.
For 
opens upward with two minimum points.
For c<0, the graph opens downward, and has an absolute minimum at x=0 and no local minimum.
d. For 
a parabola whose vertex (0, 1), is the absolute maximum.
For 
opens upward with two minimum points.
For c<0, the graph opens downward, and has an absolute maximum at x=0 and no local minimum.