Solve the system to find W1 and W2. Linear systems occur in the design of roof trusses for new homes and buildings. The simplest type of roof truss is a triangle. The truss shown in the figure is used to frame roofs of small buildings. If a force of 116 pounds is applied at the peak of the truss, then the forces or weights W1 and W2 exerted parallel to each rafter of the truss are determined by the following linear system of equations. 
 (W1 + W2) = 116 W1 - W2 = 0
(W1 + W2) = 116 W1 - W2 = 0
A. W1 = -66.97 lb; W2= -66.97 lb
B. W1 = 38.67 lb; W2= 38.67 lb
C. W1 = 66.97 lb; W2= 66.97 lb
D. W1 = 66.97 lb; W2= 58 lb
Answer: C
You might also like to view...
Solve the inequality graphically, numerically, or symbolically, and express the solution in interval notation. Where appropriate, round to the nearest tenth. ?b - 2? + 1 > 18
A. (-?, -21) ? (15, ?) B. (-15), (19) C. (-?, -15) ? (19, ?) D. (-?, -15) ? (21, ?)
Write the word statement as an equation. Use x to represent the unknown number. Do not solve.The quotient of the difference of 3 and a number and the sum of twice the number and 12, yields 3 times the number added to 39.
A. (x - 3)(2x + 12) = 39 - 3x B. (3 - x) ÷ (2x + 12) = 3x + 39 C. (3 - x)(2x + 12) = 3x - 39 D. (x - 3) ÷ (2x + 12) = 39 - 3x
Find the solution set for the equation.|5x - 6| = |x + 8|
A. 
B. 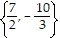
C. ?
D. 
Simplify.(7x2 + 4y)2
A. 49x2 + 56x2y + 16y2 B. 49x4 + 65x2y + 16y2 C. 49x4 + 56x2y + 16y2 D. 49x4 + 28x2y + 16y2