Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.9 + 18 + 27 + ... + 9n = 
What will be an ideal response?
First, we show the statement is true when n = 1.
For n = 1, we get 9 = 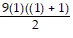 = 9.
= 9.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
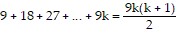 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
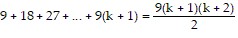 .
.
So we assume that 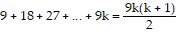 is true and add the next term,
is true and add the next term, 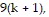 to both sides of the equation.
to both sides of the equation.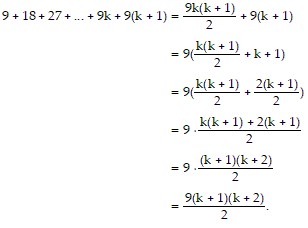
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem.The area A = ?r2 of a circular oil spill changes with the radius. At what rate does the area change with respect to the radius when 
A. 8? ft2/ft B. 16? ft2/ft C. 8 ft2/ft D. 4? ft2/ft
Provide an appropriate response.Find the equation of the line that is perpendicular to the line y = 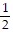 x + 5 and passes through the point (6, -4). Write the equation in standard form.
x + 5 and passes through the point (6, -4). Write the equation in standard form.
A. 2x + y = 8 B. 2x - y = 16 C. 2x + y = -10 D. x - 24 = 14
Multiply.-7x6(-5x6 + 10x5)
A. -35x6 B. 35x12 + 10x5 C. -35x12 - 35x11 D. 35x12 - 70x11
Graph the inequality.x < 2![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()