Solve the problem.Formulate the following problem as a linear programming problem (DO NOT SOLVE):A steel company produces two types of machine dies, part A and part B. Part A requires 6 hours of casting time and 4 hours of firing time. Part B requires 8 hours of casting time and 3 hours of firing time. The maximum number of hours per week available for casting and firing are 85 and 70, respectively. The company makes a $2.00 profit on each part A that it produces, and a $6.00 profit on each part B that it produces. How many of each type should the company produce each week in order to maximize its profit? (Let x1 equal the number of A parts and x2 equal the number of B parts produced each week.)
What will be an ideal response?
| Maximize | P = 2x1 + 6x2 |
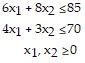
Mathematics
You might also like to view...
Solve the problem.A retailer finds that total costs per day are given by c = 81 + 225, where c is cost and n is units sold. What is c when no units are sold?
+ 225, where c is cost and n is units sold. What is c when no units are sold?
A. $306 B. $135 C. $225 D. $1215
Mathematics
Find the probability.One digit from the number 3,474,554 is written on each of seven cards. What is the probability of drawing a card that shows 5?
A. 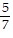
B. 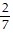
C. 1
D. 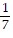
Mathematics
Solve and graph the inequality. Give answer in interval notation.-6x - 3 ? -7x - 5![]()
A. (-?, -6)![]()
B. (-6, ?)![]()
C. [-2, ?)![]()
D. (-?, -2]![]()
Mathematics
Find the domain of f.f(x) = 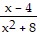
A. {x | x ? 8} B. {x | x ? -8} C. All real numbers D. {x | x ? ±2}
Mathematics