Suppose a 6-ft person wishes to determine the height of a bridge above the bottom of a canyon, as shown in the figure below. To do this, this person stands at one end of the bridge (point A) and looks down to a point directly below the other end (point B). With the help of a companion, point P is determined to form two triangles. Find the distance to the bottom of the canyon, if 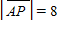 ft and
ft and
src="https://sciemce.com/media/3/ppg__cognero__7.4_Similar_Triangles__media__85d99f41-c3ea-40e6-8644-705ece164be5.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_8b5f27d438c3497ea9c20704d" /> ft.
?

?
A. 30 ft
B. 8 ft
C. 5 ft
D. 6 ft
E. 40 ft
Answer: A
Mathematics
src="https://sciemce.com/media/3/ppg__cognero__7.4_Similar_Triangles__media__85d99f41-c3ea-40e6-8644-705ece164be5.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_8b5f27d438c3497ea9c20704d" /> ft.
?
?
A. 30 ft
B. 8 ft
C. 5 ft
D. 6 ft
E. 40 ft
Answer: A
You might also like to view...
Translate the phrase into an arithmetic expression and calculate by hand.31 less than 51
A. 51 - 31 = 30 B. 51 - 31 = 15 C. 51 - 31 = 40 D. 51 - 31 = 20
Solve the problem.Give the number of possible outcomes for choosing a 4-digit number if each digit is chosen at random. The first digit may be a zero. Repetition is allowed.
A. 40 B. 100,000 C. 1000 D. 10,000
Find the equation for the tangent to the curve at the given point.f(x) = 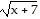 , (2, 3)
, (2, 3)
A. y = 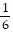 x +
x + 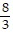
B. y = 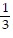 x +
x + 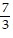
C. y = 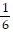 x -
x - 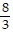
D. y = 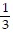 x -
x - 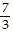
For the pair of functions, determine the domain of f + g.f(x) = 2x2 + 9, g(x) = 3x3 - 7
A. (0, ?) B. (-?, 0) or (0, ?) C. (-?, 0) D. (-?, ?)