Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.4 + 8 + 12 + ... + 4n = 2n(n + 1)
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 4 = 2(1)(1 + 1) = 4.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
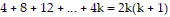 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
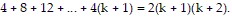
So we assume that 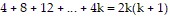 is true and add the next term,
is true and add the next term,  to both sides of the equation.
to both sides of the equation.
4 + 8 + 12 + ... + 4k + 4(k + 1) = 2k(k + 1) + 4(k + 1)
= (k + 1)(2k + 4)
= 2(k + 1)(k + 2)
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Solve the equation using the zero product property.(x - 7)(2x + 19) = 0
A. 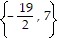
B. 
C. 
D. 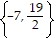
Provide an appropriate response.For a particular game at a casino, the expected winning for the player is -$0.87. How would you interpret this statement?
What will be an ideal response?
Find the exact value of y, or state that y is undefined.y = cot-1 (-1)
A. 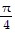
B. 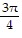
C. 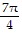
D. 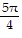
Solve the problem.How long will it take for prices in the economy to double at a 7% annual inflation rate? Round to the nearest hundredth when necessary.
A. 10.24 yr B. 23.45 yr C. 16.24 yr D. 9.01 yr